また、そのときのcosθ、tanθの値を求めよ。
(1)cosθ=−√3/2 (2)sinθ=−√2/2 (3)tanθ=√3
(4)cosθ=−1 (5)sinθ≦1/2 (6)cosθ>1/2
(1)2cos2θ+5sinθ+1=0 (2)2sin2θ−3cosθ<0
(3)2cos2θ−sinθ−1≦0
(1)tan2θ=tanθ (2)cos(θ+60°)=√3/2
(3)2cos2θ<cosθ (4)sin(θ−120°)<0
4cosθ−sin2θ=a ・・・(i)
について以下の問いに答えよ。
(1)左辺を y とおき、cosθ=t とおいて、左辺を t の式で表せ。また、 y と t の関係をグラフで示せ。
(2)方程式(i)を満たすθが存在するように、a の値の範囲を求めよ。
ただし、−90°≦θ≦90°とする。
(1)y=sinx−cosx (2)y=cosx+√3sinx
(3) sinθ+7cosθが最大となるのは、tanθ=( サ) のときで、その最大値は(シ)である。
点DをDC=BCとなるようにとる。
(1)線分ADと線分BDの長さを求めよ。
(2)線分ACと線分BDの交点 をEとするとき、sin∠AEBを求めよ。
線分ABの長さを r とする。∠AOB=θとするとき tanθ を r, p で表せ。
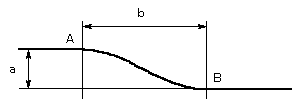
図の点Aと点Bは高さの差がa、水平距離がbであり、その間の曲線は、sin
カーブになっている。
(点A、点Bで、極大、極小になっていて、1/2
波長の波)
このとき、点Aからx離れた地点での点Bからの高さを求めよ。
劣弧BC上に点Pをとり、∠BAP=θ(0°≦θ≦60°)とする。
(1) PA・PBをr,θを用いて表せ。
(2) PA・PB + PB・PC + PC・PAの最大値およびその時のθの値を求めよ。
三角形ABCの3辺をa=BC 、b=CA 、c=ABで、内角をそのまま A,B,Cで表し、
三角形の面積をSで表すとき、次のうち正しいのはどれか?
1; S=1/2ab sinC
2; c sinB=b sinC
3; a sinB=b sinA
4; a=c sinB+b sinC
5; c=a cosB+b cosA
それぞれ5、6である台形の高さと面積を求めよ。
(1) sinx−√3cosx=0
(2) cosx−sinx=1/√2
(1)sin3θ=cos2θが成り立つことを証明せよ。
(2)sin3θをtの式で表せ。
(3)(1)と(2)よりtについての方程式を作り、tの値を求めよ。
(1)f(θ)=r・sin(θ+α)+cを満たすよう、定数rを求めよ。また、sinα、cosαの値を求めよ。
(2)0≦θ<2πのとき、関数y=f(θ)の最大値と最小値を求めよ。
(3)0≦θ≦π/2のとき、関数y=f(θ)の最大値と最小値を求めよ。
xについての2次式 f(x)=x2+2(4cosθ−1)x+1について次の問いに答えよ。
(1) 2次関数 y=f(x)の最小値をg(θ)とするとき、g(θ)の最大値を求めよ
(2) f(1)<0となるよう、θの値の範囲を定めよ
(3) 2次方程式 f(x)=0が異なる2つの解を持つように、θの値の範囲を求めよ。

赤い長方形をこの位置から、反時計回りに15°、30°、45°回転したとき、
赤い長方形の4辺またはその延長線が、黄色い長方形の辺を切る位置を求めよ。
その面積 S は
S=√(s-a)(s-b)(s-c)(s-d) 但しs=(a+b+c+d)/2
で表されることを証明せよ。
xの関数f(x)=a sinx+2cosx(0°≦x<360°)がf(240°)=2を満たしている。
(1) a=□√□である。
(2) f(x)=□sin(x+□°)である。ただし、括弧内の度数は0°以上360°未満とする。
(3) 方程式f(x)=−2√2の解はx=□°、□°である。
(4) 不等式f(x)<−2√3の解は□°<x<□°である。
問題2
AB=12、BC=5、CA=13の△ABCの辺AC上に∠BDC=60°となる点Dをとる。
∠BAC=αとすると、sinα=□/□、cosα=□/□である。
また、sin∠BCA=□/□であり、さらにsin∠DBC=□+□√□/□だか
ら、BD=□√□/□、CD=□(□+□√□)/□である。
(1)Aから辺BCに下ろした垂線とBCとの交点をEとすると、BE=(ア)/(イ)であり、BD2=(ウ)/(エ)である。
(2)三角形ABDの外接円上に、BF=1となる点Fをとり、四角形ABFDを作る。
このとき、cos∠BFD=(オ)/(カ)であり、FD=(キ)、cos∠ABF=(ク)/(ケ)である。
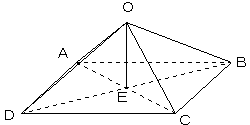
また、Oから平面ABCDに下ろした垂線と平面ABCDの交点をEとするとき、OE=√(ア)である。
さらに、線分OB,ODの中点をそれぞれG,Hとし、平面AHGと線分OC,OEの交点をそれぞれ
I,JとするときAG=(イ)、AJ=√(ウ)/(エ)である。
ここで、OI=a、JI=bとおくと、OJは∠AOIの二等分線だから、b=√(オ)/(カ)
と表され、OI=(キ)、△OIJ/△OAJ=(ク)/(ケ)である。
3直線 l:y=2x m:y=−3x+10 n:y=ax(aは定数)があり、l、mの交点をAとする。
0<a<2のときl、nのなす角をθ(0°<θ<90°)とすれば、tanθ=□−a/□+□aである。
θ=45°のとき、a=□/□であり、2直線m、nの交点をBとすれば、3点O,A,Bを通る円の方程式は
(x−□)^2+(y−□)^2=□となる。
また、∠AOBの二等分線の方程式はy=(□√□ー□/□)xである。
問題2
半径1の半円があり、直径の両端をA,Bとする。半円周上に点Pをとり、
∠PAB=θ(0°<θ<90°)とする。
また、点Pから、線分ABに垂線を下ろし、ABとの交点をHとする。
AP=□cosθ、PH=sin□θであるから、積AP・PHをsinθを用いて
表すと、AP・PH=□sin□θ+□sinθとなる。
これより、積AP・PHの最大値は□√□/□であり、このとき、sinθ=√□/□である。
問題3
平行四辺形ABCDの辺のAB上に点Eをとり、AE=4、AD=6、DE=5、
∠AED=θ、∠BEC=θ/2(0°<θ<90°)とする。
cosθ=□/□だから、sinθ=□√□/□、sinθ/2=√□/□、cosθ/2=□/□である。
また、cos∠DAE=□/□、cos3θ/2=□/□であるから、∠ADE=□θ/□である。
また、CE=□/□、BE=□/□である。
ABを3:1に内分する点をEとし、BCの中点をFとする。AFとCEの交点をGとする。
底面ABCに垂直な直線をGに立てこの直線がADを延長した直線と交わる点をHとする。
(1)AGの長さを求めよ。
(2)∠AFH=θとするときcosθの値を求めよ。
これを満たすx、yを求めなさい。
2)x=sinθ+cosθ+1、y=sin2θである時、yをxの関数で表し、かつxの変域を求めよ。
3)点(-3,2)を通り、直線3x-4y-12=0となす角が45°の直線の方程式を求めよ。
1)2cos2(x+90°)-√3cos(x+180°)+1=0 ただし 0°≦x<360°
2)cos3θ+2cosθ=0 ただし -90°<θ<90°
3)sin2x>cosx ただし 0°<x<360°
(1)∠ADB,∠DACの大きさを求めよ。
(2)線分CD,ACの長さを求めよ。
が成り立つとき三角形ABCはどんな形でしょうか?
PA=4、AB=2、CD=5となった。PDの長さを求めよ。
また、このとき2点C、Dを通る他の円にPから接線を引き、接点Tをとすると
TA=3√6であった。TBの長さを求めよ。
このとき、BCと、四角形ABCDの面積を求めよ。
辺BCの長さをxとすると、xは
x2-[ア]x-24=0
の解であり、x>0だから
BC=[イ]
である。
∠ABCの二等分線と△ABCの外接円との交点のうち、Bではない方をD、線分BCを5:3に内分する点をEとする。
直線AEと線分BDとの交点をF、直線AEと△ABCの外接円との交点のうち、Aではない方をGとする。
このとき、線分BEの長さは[ウ]だから、
∠BAG=[エオ]°,∠BFE=[カキ]°
であることがわかる。
また、
∠ADC=[クケコ]°
であることと、AD=CDであることから、
AD=サ√シ/ス
となる。よって、
DE=セ√ソ/タ
であり、線分DGと線分BCの交点をHとすると、4点D,F,E,Hが同一円周上の点であるから
FH=チ/ツ
である。