ａｋｉｒａさんからの質問１

問題
円に内接する四角形ABCDの辺BA、CDの延長の交点をPとするとき、
PA＝4、AB＝2、CD＝5となった。PDの長さを求めよ。
また、このとき2点C、Dを通る他の円にPから接線を引き、接点TをとするとTA＝3√6であった。
TBの長さを求めよ。

解答


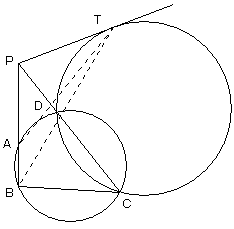
方べきの定理より、
　ＰＡ・ＰＢ＝ＰＤ・ＰＣ
よって、ＰＤ＝ｘ とおくと、
　ｘ（ｘ＋５）＝４・６＝２４
　ｘ²＋５ｘ−２４＝０
　(ｘ−３)(ｘ＋８)＝０
ｘ＞０　より、
　ｘ＝３

同じく方べきの定理より、
　ＰＴ²＝ＰＤ・ＰＣ＝２４
　ＰＴ＝２√６
△ＰＴＡ における余弦定理より、∠ＴＰＡ＝θとおくと、
　cosθ＝(ＰＡ²＋ＰＴ²−ＴＡ)/(２ＰＡ・ＰＴ)＝−７√６/４８
△ＰＴＢ における余弦定理より、
　ＴＢ²＝ＰＢ²＋ＰＴ²−２ＰＢ・ＰＴcosθ＝８１
　ＴＢ＝９

「算数・数学」の部屋に戻る