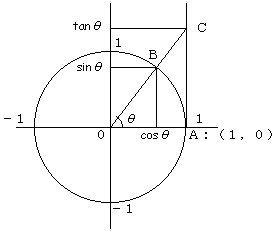
三角関数の問題を解くには、ある角度θが与えられたとき、sinθ、cosθ、tanθを
正しく計算できることが重要です。
上図のように、単位円(原点中心、半径1の円)を描き、点A:(1,0)を原点のまわりに
反時計回りに角度θだけ回転した点Bのx座標が cosθ、y座標が sinθ となり、直線OBと、
直線x=1との交点Cのy座標が tanθ となります。
にのけいさんからの質問1
1.
次の等式を満たすθの値、または、不等式を満たすθの値を求めよ。ただし、0°≦θ≦360°とする。
(1)cosθ=−√3/2
(2)sinθ=−√2/2
(3)tanθ=√3
(4)cosθ=−1
(5)sinθ≦1/2
(6)cosθ>1/2
2.
0°≦θ<360°のとき、次の方程式、不等式を満たすθの値またはθの値の範囲を求めよ。
(1)2cos2θ+5sinθ+1=0
(2)2sin2θ−3cosθ<0
(3)2cos2θ−sinθ−1≦0
3.
0°≦θ<360°のとき、次の方程式、不等式を満たすθの値、またはθの値の範囲を求めよ。
(1)tan2θ=tanθ
(2)cos(θ+60°)=√3/2
(3)2cos2θ<cosθ
(4)sin(θ−120°)<0
4.
0°≦θ<360°のとき、θについての方程式
4cosθ−sin2θ=a ・・・(i)
について以下の問いに答えよ。
(1)左辺をyとおき、cosθ=t とおいて、左辺をtの式で表せ。また、yとtの関係をグラフで示せ。
(2)方程式(i)を満たすθが存在するように、aの値の範囲を求めよ。
5.
関数y=2cos2θ+4sinθ+1の最大値、最小値とそのときのθの値を求めよ。
ただし、−90°≦θ≦90°とする。
6.
次の各場合について、y=0となるxの値、および、yの最大値を求めよ。ただし、0°≦x<180°とする。
(1)y=sinx−cosx
(2)y=cosx+√3sinx
解答
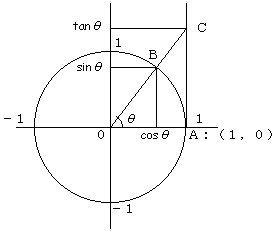
三角関数の問題を解くには、ある角度θが与えられたとき、sinθ、cosθ、tanθを
正しく計算できることが重要です。
上図のように、単位円(原点中心、半径1の円)を描き、点A:(1,0)を原点のまわりに
反時計回りに角度θだけ回転した点Bのx座標が cosθ、y座標が sinθ となり、直線OBと、
直線x=1との交点Cのy座標が tanθ となります。
1.
(1)cosθ=−√3/2
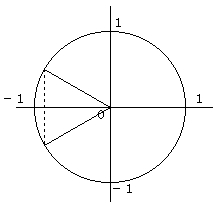
単位円上でx座標が−√3/2 となる角θは、図より
θ=150°,210°
※特殊な場合(0°,90°,180°,270°など)を除いて、θの値は2カ所あります。
(2)sinθ=−√2/2
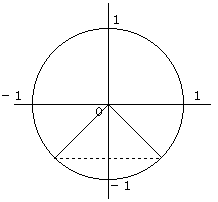
単位円上でy座標が−√2/2 となる角θは、図より θ=225°,315°
(3)tanθ=√3
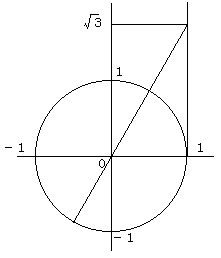
点(1,√3)を結ぶ直線と単位円の交点より、θ=60°,240°
(4)cosθ=−1
単位円上でx座標が−1になるのは θ=180° だけです。
(5)sinθ≦1/2
単位円上でy座標が1/2以下になるのは、図のような範囲です。
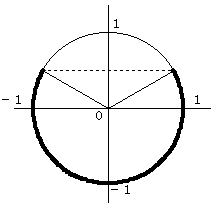
θのとるべき範囲を 0°≦θ≦360°の範囲の角度で表すと、
0°≦θ≦30° または 150°≦θ≦360°
(6)cosθ>1/2
単位円上でy座標が1/2より大きくなるのは、図のような範囲です。
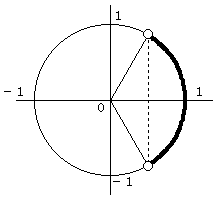
θのとるべき範囲を 0°≦θ≦360°の範囲の角度で表すと、
0°≦θ<60° または 300°<θ≦360°
境界上の角度は含まないことに注意(≦ ではなく <である)
2.
この問題を解くには、1.のような問題が確実に解けることと、いくつかの公式が使えることが
必要です。ここで使う公式は、
sin2θ+cos2θ=1・・・・・・(a)
です。
2.の3問はいずれも、
1) sinθ または cosθ の値がいくつかを求める。
2) 1.と同じように、角度θを求める
の手順です。
(1)2cos2θ+5sinθ+1=0
sin と cos の両方が混じっているので、公式(a)
を使って、cos2θ を sin2θ に
変えてしまうことを考えます。
(a) より、
cos2θ=1−sin2θ
これを、与式に代入して、
2(1−sin2θ)+5sinθ+1=0
整理して、
−2sin2θ+5sinθ+3=0
x=sinθ とおいて、整理すると、(慣れれば、xとおかなくてもできます)
2x2−5x−3=0
これを −1≦x≦1 の範囲で解いて、
(2x+1)(x−3)=0
x=−1/2
つまり、sinθ=−1/2
θ=210°、330°
(2)2sin2θ−3cosθ<0
sin2θ=1−cos2θ より、
2(1−cos2θ)−3cosθ<0
整理して(今度は x=cosθ とおかないでみます)
2cos2θ+3cosθ−2>0 (不等号の向きに注意!)
(2cosθ−1)(cosθ+2)>0
cosθ<−2 または 1/2<cosθ
−1≦cosθ≦1 であることを考慮すると、
1/2<cosθ≦1
が、求める範囲です。
これを、0°≦θ<360° の範囲で解くと、図より、
0°≦θ<60° または 300°<θ<360°

(3)2cos2θ−sinθ−1≦0
cos2θ=1−sin2θ より、
2(1−sin2θ)−sinθ−1≦0
整理して、
2sin2θ+sinθ−1≧0
(2sinθ−1)(sinθ+1)≧0
sinθ≦−1 または 1/2≦sinθ
−1≦sinθ≦1 であることを考慮すると、
sinθ=−1 または 1/2≦sinθ≦1
これを、0°≦θ<360° の範囲で解くと、
θ=270° または 30°≦θ150°
3.
考え方と手順は、2.とほとんど同じです。
(1)tan2θ=tanθ
tanθ についての2次方程式として解くと、
tan2θ−tanθ=0
tanθ(tanθ−1)=0
tanθ=0,1
tanθ=0 のとき θ=0°、180°
tanθ=1 のとき θ=45°、225°
答え:θ=0°、45°、180°、225°
(2)cos(θ+60°)=√3/2
φ=θ+60° とおくと、
cosφ=√3/2・・・(1)
を解くだけの問題です。ただし、角度の範囲が
60°≦φ<420°
である点に注意するだけです。この範囲で、(1)
を解くと、
φ=330°、390°
θ=φ−60°
より、
θ=270°、330°
(3)2cos2θ<cosθ
整理して、
2cos2θ−cosθ<0
cosθ(2cosθ−1)<0
これを解いて、
0<cosθ<1/2
よって、
0≦θ<60° または 300°≦θ<360°
(4)sin(θ−120°)<0
φ=θ−120°
とおくと、
sinφ<0 −120°≦φ<240°
−120°≦φ<0 または 180°<φ<240°
θ=φ+120°
より
0≦θ<120° または 300°<θ<360°
4.
(1)
y=4cosθ−sin2θ
とおく。
sin2θ=1−cos2θ
より、
y=4cosθ−(1−cos2θ)
t=cosθ とおくと、
y=t2+4t−1・・・(i)
y=(t+2)2−5
より、(i) のグラフは、y=t2 のグラフをx軸方向に−2、y軸方向に−5 移動したグラフとなる。
但し −1≦t≦1
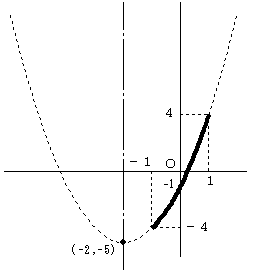
(2)
(1)のグラフより
−4≦a≦4
5.
倍角の公式より、
y=2cos2θ+4sinθ+1
=2(1−2sin2θ)+4sinθ+1
t=sinθ とおくと、
y=−4t2+4t+3 −1≦t≦1
y=f(t) とおくと、
f(t)=−4(t−1/2)2+4
f(-1)=−5、f(1/2)=4、f(1)=3
より、
t=−1 つまり θ=−90° のとき 最小値 −5
t=1/2 つまり θ=30° のとき 最大値 4
6.
この問題は、三角関数の加法定理を使う問題です。
(1)y=sinx−cosx
cos(-45°)=√2/2 sin(-45°)=−√2/2
に対し、
y=√2{cos(-45°)sinx+sin(-45°)cosx}
が成り立ちます。三角関数の加法定理より、
y=√2sin(x−45°)
0°≦x<180°
のとき、
−45°≦x−45°<135°
であり、y=0となるのは、x−45°=0 つまり x=45°のとき
また、x−45°=90° つまり x=135°のとき yの最大値√2
(2)y=cosx+√3sinx
sin30°=1/2 cos30°=√3/2
に対し、
y=2(sin30°cosx+cos30°sinx)
が成り立ちます。三角関数の加法定理より、
y=2sin(x+30°)
0°≦x<180°
のとき、
30°≦x+30°<210°
であり、y=0となるのは、x+30°=180° つまり x=150°のとき
また、x+30°=90° つまり x=60°のとき yの最大値2
sin(α+β)=sinαcosβ+cosαsinβ
sin(α−β)=sinαcosβ−cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ
cos(α−β)=cosαcosβ+sinαsinβ
tan は省略
また (α+β)を含む式で α=β とおくと、2倍角の公式ができます。
倍角の公式
sin2α=2sinαcosα
cos2α=cos2α−sin2α
=2cos2α−1
=1−2sin2α
加法定理の応用(名前は知りません)
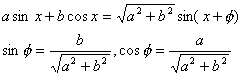
こちらの方の公式は、そのまま覚えるのは大変なので、以下のようにして、
公式の成り立ちを、よく理解してください。
もし、asinx+bcosx の、係数a、bについて
a=cosy、b=siny
となるような角度yが存在すれば、加法定理によって、ただちに
asinx+bcosx=cosysinx+sinycosx=sin(x+y)
と書けます。
ところが、一般にはそのようにはなりません。
2実数a、bが、
a=cosy、b=siny
の形になるためには、
a2+b2=1
が成り立たなければなりません。
任意の2実数a、bについて、これは必ずしも成り立ちませんが、
a2+b2≠0
のとき、
a'=a/√(a2+b2) b'=b/√(a2+b2)
とおくと、a'、b' は、
a'2+b'2=1
を満たし、ある角度φについて、
a'=cosφ、b'=sinφ
とおくことができます。これを用いて
asinx+bcosx
を変形すると、
asinx+bcosx=√(a2+b2){a'sinx+b'cosx}
=√(a2+b2){cosφsinx+sinφcosx}
=√(a2+b2)sin(x+φ)
となります。
上記の問題では、角度φを具体的に見つけていくことがポイントになります。