問題
a=5,b=6,c=7である、△ABCにおいて、辺ABのBの側への延長線,辺BC,辺CAのCの側への延長線に接する円Oの半径を求めて下さい。
解答
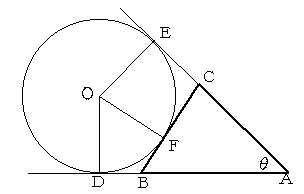
図のように接点をD,E,F とし、円の中心をOとします。
BD=BF,CE=CF より、
AE+AD=AB+AC+(BD+CE)=AB+AC+(BF+CF)
=AB+BC+CA=5+6+7=18
AD=AEより、
AD=AE=9
θ=∠BAC とおくと、余弦定理より、
cosθ=(62+72-52)/(2・6・7)=5/7
半角の公式
cos2(θ/2)=(cosθ+1)/2
より、
cos2(θ/2)=6/7
0<θ<90°より、cosθ>0
よって、
cosθ=√(6/7)
また、sin2θ+cos2θ=1 より
sinθ=√(1/7)
tanθ=sinθ/cosθ=√(1/6)
よって、tanθ=OD/AD より、
OD=AD×tanθ=9×√(1/6)=3√6/2
算数・数学の部屋に戻る