問題
AD//BC,AD=12,BC=40,AB=17,CD=25の台形の面積を求めて下さい。
解答
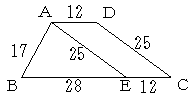
図のように、AからDCに平行な直線とBCの交点をEとします。
このとき、平行四辺形AECDは△ABEの面積の 6/7 倍になりますから、
△ABEの面積の 13/7 倍が台形ABCDの面積になります。
ヘロンの公式より、
(17+25+28)/2=35 に対して
△ABE=√{35(35-17)(35-25)(35-28)}=210
よって、
台形ABCD=210×(13/7)=390
別解
△ABEにおいて、θ=∠ABE とおくと、余弦定理より
cosθ=(172+282-252)/(2・17・28)=8/17
0<θ<π より、sinθ>0 だから
sinθ=√(1-cos2θ)=15/17
三角形の面積の公式より、
△ABE=17・28・(15/17)/2=210
よって、
台形ABCD=210×(13/7)=390
算数・数学の部屋に戻る