問題
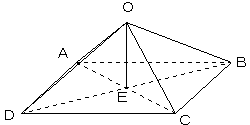
底面がAB=CD=8,AD=BC=6の長方形で、OA=OB=OC=OD=6である四角錘OABCDを考える。
また、Oから平面ABCDに下ろした垂線と平面ABCDの交点をEとするとき、OE=√(ア)である。
さらに、線分OB,ODの中点をそれぞれG,Hとし、平面AHGと線分OC,OEの交点をそれぞれ
I,JとするときAG=(イ)、AJ=√(ウ)/(エ)である。
ここで、OI=a、JI=bとおくと、OJは∠AOIの二等分線だから、b=√(オ)/(カ)
と表され、OI=(キ)、△OIJ/△OAJ=(ク)/(ケ)である。
解答
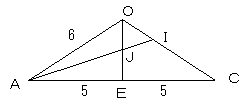
3点A,C,Oを通る平面で、この四角錐を切ると、断面は上のようになります。
ACは三平方の定理により10であり、EはACの中点なので、
AE=EC=5
です。よって、
OE=√(62−52)=√11………(ア)の答え
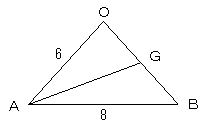
AGは△OABの点Aからの中線なので、中線定理より、
AB2+AO2=2(AG2+BG2)
64+36=2(AG2+9)
AG2=41
AG=√41………(イ)の答え
3点G,H,J はいずれも△OBD上にあり、これとは異なる平面AHG上にあるので、
GHJは、同一直線上にあります。つまり、JはGHの中点であり、OEの中点にもなります。
△AEJにおける三平方の定理より、
AJ2=AE2+JE2=25+11/4=111/4
AJ=√111/2………√(ウ)/(エ)の答え
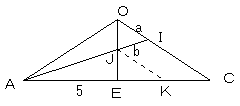
Jから、OCに平行な線を引きACとの交点をKとします。
KはECの中点なので、
AJ:JI=AK:KC=3:1
よって、b=JI=AJ÷3=√111/6………√(オ)/(カ)の答え
OJは∠AOIの二等分線なので、OA:OI=AJ:JI=3:1
よって、OI=6÷3=2………(キ)の答え
△OIJ/△OAJ=IJ/AJ=1/3………(ク)/(ケ)の答え
算数・数学の部屋に戻る