柳屋さんからの質問７

問題１
３直線　ｌ：ｙ＝２ｘ　ｍ：ｙ＝−３ｘ＋１０　ｎ：ｙ＝ａｘ（ａは定数）があり、ｌ、ｍの交点をＡとする。
０＜ａ＜２のときｌ、ｎのなす角をθ（０°＜θ＜９０°）とすれば、ｔａｎθ＝□−ａ/□＋□ａである。
θ＝４５°のとき、ａ＝□/□であり、２直線ｍ、ｎの交点をＢとすれば、３点Ｏ，Ａ，Ｂを通る円の方程式は
（ｘ−□）＾２＋（ｙ−□）＾２＝□となる。
また、∠ＡＯＢの二等分線の方程式はｙ＝（□√□ー□/□）ｘである。

解答１

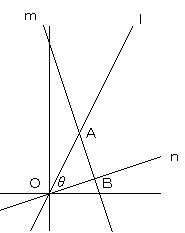
直線 ｌ の角度をα、直線 ｎ の角度をβとすると、
　θ＝α−β
です。直線の傾きより、
　tanα＝２，tanβ＝ａ
三角関数の加法定理より、
　tanθ＝tan(α−β)＝(tanα−tanβ)/(１＋tanαtanβ)
　　＝(２−ａ)/(１＋２ａ)

θ＝４５°のとき、tanθ＝１ なので、
　(２−ａ)/(１＋２ａ)＝１　より、
　ａ＝1/3

このとき、ｍとｎは直行するので、求める円の中心はＯＡの中点、半径はＯＡの半分である。
ｌとｍを連立させると、(x,y)=(2,4) より、円の中心は(1,2)、半径は√５。
よって、円の式は
　(ｘ−１)²＋(ｙ−２)²＝５

Ｂの座標は、（３，１）。
角の二等分線の定理より、求める直線は、
ＡＢを √２：１ に内分する点を通る。その点は、
　(３√２＋２，√２＋４)/(√２＋１)
よって、その傾きは、
　(√２＋４)/(３√２＋２)＝(５√２−１)/７
求める式は、
　ｙ＝{(５√２−１)/７}ｘ


問題２
半径１の半円があり、直径の両端をＡ，Ｂとする。半円周上に点Ｐをとり、
∠ＰＡＢ＝θ（０°＜θ＜９０°）とする。
また、点Ｐから、線分ＡＢに垂線を下ろし、ＡＢとの交点をＨとする。
ＡＰ＝□ｃｏｓθ、ＰＨ＝ｓｉｎ□θであるから、積ＡＰ・ＰＨをｓｉｎθを用いて
表すと、ＡＰ・ＰＨ＝□ｓｉｎ^□θ＋□ｓｉｎθとなる。
これより、積ＡＰ・ＰＨの最大値は□√□/□であり、このとき、ｓｉｎθ＝√□/□である。

解答２

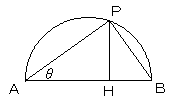
　ＡＰ＝ＡＢcosθ＝２cosθ
　ＰＨ＝ＡＰsinθ＝２sinθcosθ＝sin２θ
よって、
　ＡＰ・ＰＨ＝２cosθsin２θ＝４sinθcos²θ＝４sinθ(１−sin²θ)
　　＝−４sin³θ＋４sinθ
ｘ＝sinθ とおくと、
　ＡＰ・ＰＨ＝−４ｘ³＋４ｘ
ｆ（ｘ）＝−４ｘ³＋４ｘ を ０＜ｘ＜１ の範囲で最大値を求める。
　ｆ’（ｘ）＝−１２ｘ²＋４＝０
を解くと、ｘ＝±√３/３
　０＜ｘ＜１ より、ｘ＝sinθ＝√３/３ で最大となり、最大値は
　f(√３/３)＝８√３/９

問題３
平行四辺形ＡＢＣＤの辺のＡＢ上に点Ｅをとり、ＡＥ＝４、ＡＤ＝６、ＤＥ＝５、
∠ＡＥＤ＝θ、∠ＢＥＣ＝θ/２（０°＜θ＜９０°）とする。
ｃｏｓθ＝□/□だから、ｓｉｎθ＝□√□/□、ｓｉｎθ/２＝√□/□、ｃｏｓθ/２＝□/□である。
また、ｃｏｓ∠ＤＡＥ＝□/□、ｃｏｓ３θ/２＝□/□であるから、∠ＡＤＥ＝□θ/□である。
また、ＣＥ＝□/□、ＢＥ＝□/□である。

解答３

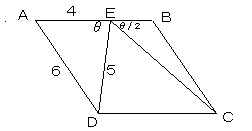
第２余弦定理より、
　cosθ＝(ＡＥ²＋ＤＥ²−ＡＤ²)/２ＡＥ・ＤＥ＝１／８
sinθ＞０より、
　sinθ＝√(1-1/64)＝３√７/８
半角の公式より
　sin²(θ/２)＝(１−cosθ)/２＝７／１６
　sin(θ/２)＝√７/４
　cos²(θ/２)＝(１＋cosθ)/２＝９/１６
　cos(θ/２)＝３／４

再び、第２余弦定理より、
　cos∠ＤＡＥ＝９/１６
一方
　cos(３θ/２)＝cos(θ＋θ/２)＝cosθcos(θ/２)−sinθsin(θ/２)
　　＝−９/１６
cos∠ＤＡＥ＝−cos(３θ/２) より、
　∠ＤＡＥ＝π−３θ/２
よって、
　∠ＡＤＥ＝π−∠ＡＥＤ−∠ＤＡＥ＝π−θ−(π−３θ/２)＝θ/２

∠ＥＢＣ＝π−∠ＤＡＥ＝３θ/２ より、sin∠ＥＢＣ＝５√７/１６
正弦定理から、
　ＢＣ/sin∠ＢＥＣ＝ＣＥ/sin∠ＥＢＣ
ＢＣ＝６、sin∠ＢＥＣ＝sin(θ/２)＝√７/４、sin∠ＥＢＣ＝５√７/１６　より、
　ＣＥ＝１５/２
∠ＢＣＥ＝π−∠ＥＢＣ−∠ＢＥＣ＝π−２θ　より、
　sin∠ＢＣＥ＝sin２θ＝２sinθcosθ＝３√７/３２
正弦定理より、
　ＢＥ/sin∠ＢＣＥ＝ＢＣ/sin∠ＢＥＣ
sin∠ＢＣＥ＝３√７/３２、ＢＣ＝６、sin∠ＢＥＣ＝√７/４ より、
　ＢＥ＝９/４

算数・数学の部屋に戻る