問題
△ABCにおいて、AB=5,AC=7,∠ABC=60°とする。
辺BCの長さをxとすると、xは
x2-[ア]x-24=0
の解であり、x>0だから
BC=[イ]
である。
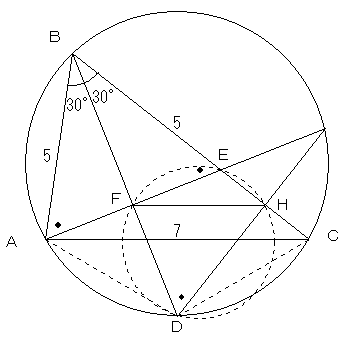
∠ABCの二等分線と△ABCの外接円との交点のうち、Bではない方をD、線分BCを5:3に内分する点をEとする。
直線AEと線分BDとの交点をF、直線AEと△ABCの外接円との交点のうち、Aではない方をGとする。
このとき、線分BEの長さは[ウ]だから、
∠BAG=[エオ]°,∠BFE=[カキ]°
であることがわかる。
また、
∠ADC=[クケコ]°
であることと、AD=CDであることから、
AD=サ√シ/ス
となる。よって、
DE=セ√ソ/タ
であり、線分DGと線分BCの交点をHとすると、4点D,F,E,Hが同一円周上の点であるから
FH=チ/ツ
である。
解答
△ABCにおける余弦定理より
72=x2+52−2・5・xcos∠ABC
整理して
x2−5x−24=0 ・・・[ア]
これを解いて、
(x−8)(x+3)=0
x>0 より
x=8 ・・・[イ]
この時点で、CE=3,BE=5 ・・・[ウ] が決まります。
△ABEは正三角形となり
∠BAG=60° ・・・[エオ]
∠BFE=90° ・・・[カキ]
四角形ABCDは円に内接するので、
∠ADC=180°−∠ABC=120° ・・・[クケコ]
△ACDは、頂角が120°の二等辺三角形であり、3辺の比は、1:1:√3 なので、
AD=7÷√3=7√3/3 ・・・[サシス]
△ADEにおいて、DFは、AEの垂直二等分線になっているので、△ADEは、AD=DE の二等辺三角形。
よって、
DE=AD=7√3/3 ・・・[セソタ]
円に内接する四角形DFEHにおいて、
∠DFE=90° より、∠DHE=90°
AD=DE=DC より、△EDCは二等辺三角形であり、DHは、CEの垂直二等分線になるので、
CH=HE
これと、AF=FE と合わせて、中点連結定理より、
FH=AC/2=7/2 ・・・[チツ]
算数・数学の部屋に戻る