りこさんからの質問１

問題
半径がrの円に正三角形ABCが内接している。
劣弧BC上に点Pをとり、∠BAP=θ(0°≦θ≦60°)とする。
　(1) PA・PBをr,θを用いて表せ。
　(2) PA・PB　+　PB・PC　+　PC・PAの最大値およびその時のθの値を求めよ。

解答

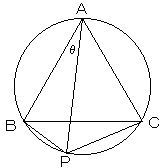
上図において、ＡＢ＝ＢＣ＝ＣＡ＝(√３)ｒ である。
また∠ＡＰＢ＝60°、∠ＡＢＰ＝120°-θ 、∠ＡＰＣ＝60°、∠ＣＡＰ＝60°-θ である。
(1) 正弦定理より
　　ＰＡ＝２ｒsin∠ＡＢＰ＝２ｒsin(120°-θ)
　　ＰＢ＝２ｒsinθ
　よって、ＰＡ・ＰＢ＝４ｒ²sin(120°-θ)sinθ
(2) 同様に、
　　ＰＣ＝２ｒsin(60°-θ)
　よって、
　　ＰＡ・ＰＢ＋ＰＢ・ＰＣ＋ＰＣ・ＰＡ＝４ｒ²{sin(120°-θ)sinθ+sinθsin(60°-θ)+sin(60°-θ)sin(120°-θ)}
　三角関数の和積の公式の１つ
　　sinαsinβ＝-{cos(α+β) - cos(α-β)}/2
　より、
　　(与式)＝-２ｒ²{cos120°-cos(120°-2θ)+cos60°-cos(2θ-60°)+cos(180°-2θ)-cos(-60°)}
　さらに、三角関数の和積の公式の１つ
　　cosα+cosβ＝2cos{(α+β)/2}cos{(α-β)/2}
　より、
　　(与式)＝-２ｒ²{cos120°-2cos30°cos(90°-2θ)-cos2θ}
　　　　　＝-２ｒ²(-1/2-√3sin2θ-cos2θ)
　　　　　＝ｒ²＋４ｒ²(√3sin2θ+cos2θ)/2
　　　　　＝ｒ²＋４ｒ²sin(2θ+30°)
　最後の行の変形は、三角関数の合成公式
　　ａsinθ+ｂsinθ=√(ａ²+ｂ²)sin(θ+α) 　sinα=ｂ/√(ａ²+ｂ²)、cosα=ａ/√(ａ²+ｂ²)
　による。
　0°≦θ≦60°の範囲で、４ｒ²sin(2θ+30°)が最大となるのは、sin(2θ+30°)=1 のとき、つまり
　　2θ+30°=90°
　　θ=30°
　このとき、
　　(与式)=５ｒ²

「算数・数学」の部屋に戻る