問題
正12、20面体は五角形、三角形をそれぞれ何度かたむけたらよいか教えてください。
解答
正十二面体の場合
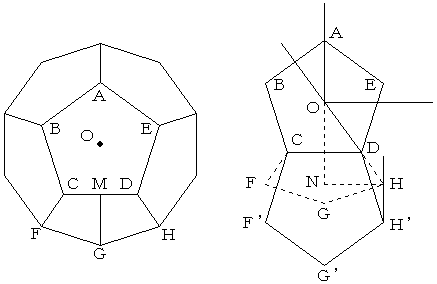
上図の左は、正十二面体のひとつの面に対して、垂直な方向から見たときの図です。
Oは、正五角形ABCDEの中心(外接円の中心)です。
この図において、OF=OG=OHであり、外周は正十角形です。
CDの中点をMとおいたときの、MGの長さを求めます。
OA=OB=OC=OD=OE=1とおきます。
上図右は、正五角形CF'G'H'D を折り返す前の図です。
正五角形CF'G'H'Dを、CDに対して折り返すので、HH' は、CDに対して、
垂直になります。つまり、Hは、EH' 上にあります(x座標が等しい)。
OE=1
より、Oを原点としたときのEのx座標は、cos18° 五倍角の公式参照
また、図形の対称性より、Hは、ODの延長上にある。
△ONHにおいて、NH=cos18° ∠NOH=36° より、
OH=cos18°÷sin 36°=√{(3+√5)/2}=(√5+1)/2
OGも同様に
OG=(√5+1)/2
一方、
OM=OD×cos36°=(√5+1)/4
より、
MG=OG−OM=(√5+1)/2−(√5+1)/4=(√5+1)/4
また、
AM=OA+OM=1+(√5+1)/4=(√5+5)/4
よって、
AM:MG=√5:1
以上より、A−O−M−Gにいたる線の断面図は以下のようになります。
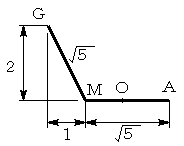
よって、五角形と五角形の角度は、上図のような角度になります。
答え Cos-1(-1/√5)≒116°
正二十面体の場合
正二十面体は、正三角形五つで、正五角錐を作りますが、下図はその正五角形を
真上から見た図です。
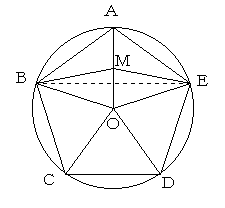
AOの中点をMとするとき、△BEMにおいて、∠BMEが求める角です。
AB=BC=CD=DE=EA=2 とおきます。
BE=2AEsin54°=√5+1
BM=EM=√3
より、三角形BEMは、以下のような形になります。
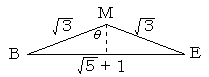
上図のようにθを決めると、
sinθ=(√5+1)/2√3=(√15+√3)/6
θ=Sin-1{(√15+√3)/6}≒69°
よって、求める角度は2θであるので、
答え 約138°
「算数・数学」の部屋に戻る