問題
1)0°≦x≦360°の時、sin2x+cosx-1の最大値と最小値を求めよ。
2)x=sinθ+cosθ+1、y=sin2θである時、yをxの関数で表し、かつxの変域を求めよ。
3)点(-3,2)を通り、直線3x-4y-12=0となす角が45°の直線の方程式を求めよ。
解答
1)
sin2x+cos2x=1 より、
sin2x+cosx-1=(1−cos2x)+cosx−1=−cos2x+cosx
X=cosx とおくと、この問題は、
f(X)=−X2+X
の、−1≦X≦1 における、最大値、最小値を求める問題となります。
f(X)=−(X−1/2)2+1/4
より、X=1/2 で最大値 f(1/2)=1/4、X=−1 で最小値 f(-1)=−2
これを、xで表すと、
答え x=60°または300°のとき、最大値1/4、x=180°のとき 最小値−2
2)
x=sinθ+cosθ+1
移項して
x−1=sinθ+cosθ
両辺2乗して
(x−1)2=sin2θ+cos2θ+2sinθcosθ=1+sin2θ
よって、
(x−1)2=1+y
y=x2−2x
また、xの変域は、合成公式より
x=sinθ+cosθ+1=√2sin(θ+45°)+1
よって、
−√2+1≦x≦√2+1
3)
ベクトルの内積を使う方法
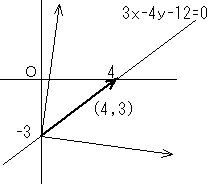
直線3x-4y-12=0 の方向ベクトルは、(4,3)、ベクトルの大きさは5。
求める直線の傾きをa とすると、その方向ベクトルは、(1,a)、ベクトルの大きさは√(1+a2)
両者の内積をとると、
成分による表し方:4・1+3・a=4+3a
ベクトルの大きさとなす角による表し方:5・√(1+a2)×cos45°
よって、
4+3a=5√(1+a2)×√2/2
両辺2乗して
9a2+24a+16=25(1+a2)/2
両辺2を掛けて
18a2+48a+32=25+25a2
移項して
7a2−48a−7=0
(7a+1)(a−7)=0
よって、
a=7 または a=-1/7
よって、点(-3,2) を通る式を作ると、
y−2=7(x+3) または y−2=−(x+3)/7
よって、
7x−y+23=0 または x+7y−11=0
図形的に求める方法
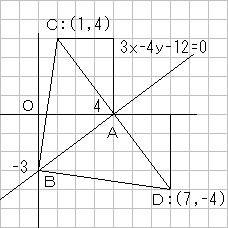
図のように∠BAC=90°AB=AC、∠BAD=90°、AB=AD
となるような点C、Dをとると、BCおよび、BDが求める直線の傾きである。
座標より、傾きを読みとると、7 または −1/7 である。
(以下同様)
「算数・数学」の部屋に戻る