問題
xy平面上において、点(p,0)を通る直線と放物線y^2=4px(p>0)の交点をA,Bとし、
線分ABの長さを r とする。∠AOB=θとするとき tanθ を r, p で表せ。
解答
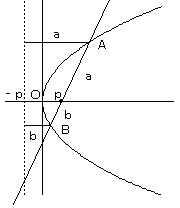
点(p,0) は、この放物線の焦点であるので、準線x=−pに対して、放物線の性質
「放物線上の任意の点から、焦点までの距離と、準線までの距離が等しい」 より、
図のように、長さa、bを決めます。
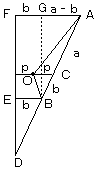
このとき、上図のような△ADFにおいて、
AF:AD=AG:AB=(a-b):(a+b)
さらに、三平方の定理より、
AF:AD:FD=(a-b):(a+b):2√(ab)
ここで、
r=a+b
p=ab/(a+b)
である。(導出省略)
一方、
∠AOB=∠AOC+∠BOC
より、まず、∠AOC、∠BOCの正接を求める。
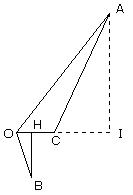
△AOIにおいて、
tan∠AOC=AI/OI
ここで、
AI=a×2√(ab)/(a+b)=2a√(ab)/(a+b)
OI=a-p=a2/(a+b)
よって、
tan∠AOC=2√(ab)/a
△BOHにおいて、
tan∠BOC=BH/OH
ここで、
BH=b×2√(ab)/(a+b)=2b√(ab)/(a+b)
OH=b-p=b2/(a+b)
よって、
tan∠BOC=2√(ab)/b
三角関数の加法定理より、
tan∠AOB=(tan∠AOC+tan∠BOC)/(1-tan∠AOC・tan∠BOC)
=2√(ab)・(a+b)/-3(ab)=-2/3・√(r/p)
「算数・数学」の部屋に戻る