三角さんからの質問１

問題
　sin18°の値を求めたい。θ＝18°、ｔ＝sinθ＝sin18°とおくとき、次の各問いに答えよ。
（1）sin3θ＝cos2θが成り立つことを証明せよ。
（2）sin3θをｔの式で表せ。
（3）（1）と（2）よりｔについての方程式を作り、ｔの値を求めよ。

解答

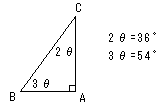
(1) 公式　sin(90°-x)＝cosx
　より、明らかですが、定義にかえって考えると、
　2θ(36°), 3θ(54°) によって、図のような直角三角形が出来ます。
　　sin3θ＝AC/BC
　　cos2θ＝AC/BC
　よって、sin3θ＝cos2θが成り立つ。

(2) sin2θ＝2sinθcosθ
　　cos2θ＝1-2sin²θ
　を利用します。
　sin3θ＝sin(θ＋2θ)＝sinθcos2θ＋cosθsin2θ
　　＝sinθ(1-2sin²θ)＋2sinθcos²θ
　　＝sinθ-2sin³θ＋2sinθ(1-sin²θ)
　　＝sinθ-2sin³θ＋2sinθ-2sin²θ
　　＝3sinθ-4sin³θ
　よって、
　　sin3θ＝3t-4t³

(3) cos2θ＝1-2sin²θ＝1-2t²
　より、
　　sin3θ＝1-2t²
　(2) の結果と合わせて
　　3t-4t³＝1-2t²
　　4t³-2t²-3t+1=0
　左辺は t=1 で０になるので、(t-1) で因数分解して
　　(t-1)(4t²+2t-1)=0
　4t²+2t-1=0 を解いて、
　　t=(-1±√5)/4
　0＜t＜1 より、
　　t=(√5-1)/4

算数・数学の部屋に戻る