問題1
xの関数f(x)=a sinx+2cosx(0°≦x<360°)がf(240°)=2を満たしている。
(1) a=□√□である。
(2) f(x)=□sin(x+□°)である。ただし、括弧内の度数は0°以上360°未満とする。
(3) 方程式f(x)=−2√2の解はx=□°、□°である。
(4) 不等式f(x)<−2√3の解は□°<x<□°である。
解答1
sin240°=-√3/2 、cos240°=-1/2 である。
(1) f(240°)=-(√3/2)a−1=2 より、
-(√3/2)a=3
a=-2√3
(2) f(x)=(-2√3)sinx+2cosx
合成の公式より、
f(x)=4{(-√3/2)sinx+(1/2)cosx}
=4(cos150°sinx+sin150°cosx)
=4sin(x+150°)
(3) f(x)=4sin(x+150°)=−2√2 より、
sin(x+150°)=−√2/2
x+150°=225°,315°
よって、
x=75°,165°
(4) 4sin(x+150°)<−2√3 より、
sin(x+150°)<−√3/2
240°<x+150°<300°
よって、
90°<x<150°
問題2
AB=12、BC=5、CA=13の△ABCの辺AC上に∠BDC=60°となる点Dをとる。
∠BAC=αとすると、sinα=□/□、cosα=□/□である。
また、sin∠BCA=□/□であり、さらにsin∠DBC=□+□√□/□だか
ら、BD=□√□/□、CD=□(□+□√□)/□である。
解答2
∠BCA=βとおきます。
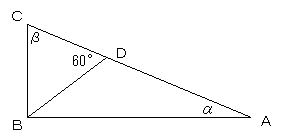
三平方の定理より、△ABCは、∠B=90°の直角三角形である。
sinα=BC/AC=5/13、cosα=AB/AC=12/13
sin∠BCA=sinβ=AB/AC=12/13、cosβ=5/13
sin∠DBC=sin(120°−β)=sin120°cosβ−cos120°sinβ
=√3/2×5/13+1/2・12/13=(12+5√3)/26
BD/sinβ=CB/sin∠BDC より、
BD=CBsinβ/sin60°=5(12/13)/(√3/2)=40√3/13
CD/sin∠DBC=CB/sin∠BDC より、
CD=CBsin∠DBC/sin60°=5(12+5√3)/26/(√3/2)=5(5+4√3)/13
算数・数学の部屋に戻る