(1) A<90° かつ C<90° の場合
(2) A>90° の場合
(3) C>90° の場合
(4) A=90° の場合
(5) C=90° の場合
通常は、(1) だけを証明して、「同様にして、(2)〜(5)の場
合も証明できる。」としても良いと思いますし、(4) は (2)
に、(5) は (3)に含めてしまっても良いと思いますが、ここ
では、すべての場合について、証明します。
TANEさんからの質問1
問題1: ΔABCにおいて、等式ccosA+acosC=b が成り立つことを示せ。
問題2: 5個の文字a,a,b,b,c から3個の文字を選んで、1列に並べる方法は何通りあるか?
答1)
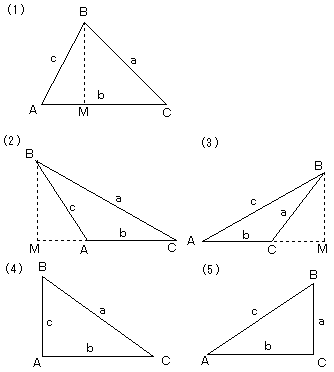
| 形状によって、以下の5通りがあります。 (1) A<90° かつ C<90° の場合 (2) A>90° の場合 (3) C>90° の場合 (4) A=90° の場合 (5) C=90° の場合 通常は、(1) だけを証明して、「同様にして、(2)〜(5)の場 合も証明できる。」としても良いと思いますし、(4) は (2) に、(5) は (3)に含めてしまっても良いと思いますが、ここ では、すべての場合について、証明します。 |
 |
(1) の場合
点Bから辺ACに下ろした垂線の足をMとします。
AM=ccosA,MC=acosC
より、
b=AM+MC=ccosA+acosC
(2) の場合
点Bから直線ACに下ろした垂線の足をMとします。
MA=ccos(180°−A)=−ccosA,MC=acosC
より、
b=MC−MA=acosC+ccosA
(3) の場合
点Bから直線ACに下ろした垂線の足をMとします。
AM=ccosA,CM=acos(180°−C)=−acosC
より、
b=AM−CM=ccosA+acosC
(4) の場合
cosA=0
なので、
b=ccosA+acosC
は明らか。
(5) の場合
cosC=0
なので、
b=ccosA+acosC
は明らか。
以上、証明終わり。
答2)
・文字が3種類の場合(a,b,cを1個ずつ選ぶ)
abc,acb,bac,bca,cab,cba
の6通り。
・文字が2種類の場合
文字の選び方は
(a,a,b)(a,a,c)(b,b,a)(b,b,c)
の4通り。
例えば、(a,a,b)の3個を選んだとき、並べ方は
aab,aba,baa
の3通り。
合計4×3=12(通り)
・両方合わせて 6+12=18 答 18通り