問題
関数f(θ)=sinθ+3√2cos(θ-π/4)+1の最大値及び最小値を求めたい。このとき、次の各問いに答えよ。
(1)f(θ)=r・sin(θ+α)+cを満たすよう、定数rを求めよ。また、sinα、cosαの値を求めよ。
(2)0≦θ<2πのとき、関数y=f(θ)の最大値と最小値を求めよ。
(3)0≦θ≦π/2のとき、関数y=f(θ)の最大値と最小値を求めよ。
解答
(1)
3√2cos(θ-π/4)=3√2{cosθcos(π/4)+sinθsin(π/4)}
=3(cosθ+sinθ)
よって、
f(θ)=sinθ+3(cosθ+sinθ)+1
=4sinθ+3cosθ+1
sinα=3/5、cosα=4/5 である角αにおいて、
sin(θ+α)=sinθcosα+cosθsinα=(4sinθ+3cosθ)/5
よって、
f(θ)=5sin(θ+α)+1
答え r=5、sinα=3/5、cosα=4/5
(2)
0≦θ<2πのとき、sin(θ+α)は1周期分カバーするので
θ=π/2−α のとき 最大値 6
θ=3π/2−α のとき 最小値 −4
(3)
0≦θ<π/2のとき、θ+αの範囲は以下の図の通り。
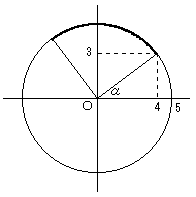
θ=π/2−α のとき、最大値 6
θ=0 のとき 最小値 4
算数・数学の部屋に戻る