問題
点(0,1)を通り、直線x+2y+2=0とのなす角が60度であるような直線の方程式を求めよ。
解答
ベクトルを使う方法が一般的ですが、三角関数の加法定理の単元ということで、
それを使います。
求める直線の傾きさえわかれば、(0,1) を通るようにするのはすぐ出来ますので、
まず傾きを求めます。
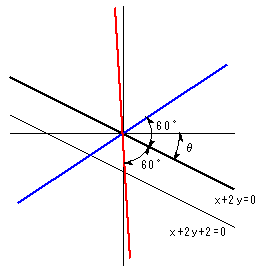
求める直線は上図の青、赤の2本あります。
x+2y+2=0 の角度をθとすると、
cosθ=2/√5、sinθ=−1/√5
青い直線の角度をφとすると、
φ=θ+60°
赤い直線の角度をψとすると、
ψ=θ−60°
また、各直線の傾きはそれぞれ tanφ、tanψ で表される。
cosφ=cos(θ+60°)=cosθcos60°−sinθsin60°
=1/√5+√3/2√5
sinφ=sin(θ+60°)=sinθcos60°+cosθsin60°
=−1/2√5+√3/√5
より、
tanφ=sinφ/cosφ=(−1+2√3)/(2+√3)=5√3−8
よって、青い直線の式は
y=(5√3−8)(x−1)
cosψ=cos(θ−60°)=cosθcos60°+sinθsin60°
=1/√5−√3/2√5
sinψ=sin(θ−60°)=sinθcos60°−cosθsin60°
=−1/2√5−√3/√5
より、
tanψ=sinψ/cosψ=(−1−2√3)/(2−√3)=−5√3−8
よって、赤い直線の式は
y=(−5√3−8)(x−1)
※tan の加法定理より、即座に
tanφ=tan(θ+60°)=(tanθ+tan60°)/(1−tanθtan60°)
=(-1/2+√3)/(1+√3/2)=(−1+2√3)/(2+√3)=5√3−8
などとしても、解けますが、tan は、sin、cos の生成物として扱った方が、
覚える公式も少なくてすみます。
算数・数学の部屋に戻る