YUさんからの質問

問題
AB=2、BC=√2、CA=√8である三角形ABC があり、この三角形の外接円の弧AC(点Bを含まない方の弧）上に、
点DをDC=BCとなるようにとる。
（1）線分ADと線分BDの長さを求めよ。
（2）線分ACと線分BDの交点 をEとするとき、sin∠ＡＥＢを求めよ。

解答

(1)
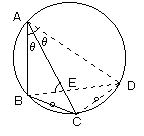
ＢＣ＝ＣＤより、それぞれに立つ円周角は等しくそれらをθとおく。
△ＡＢＣにおいて、余弦定理より、
　cosθ=(AB²+AC²-BC²)/(2・AB・AC)=(4+8-2)/(2・2・2√2)=5/4√2　・・・(1)
一方、△ＡＣＤにおける、余弦定理より、
　cosθ=(AD²+AC²-BC²)/(2・AD・AC)=(AD²+8-2)/(2・AD・2√2)=5/4√2
整理して、
　AD²-5AD+6=0
　(AD-2)(AD-3)=0
これを解いて、
　AD=2 または AD=3
AD=2 は △ＡＢＣの形状の場合の数値であるので、この場合は、AD=3 のみが答えである。

　cos2θ=2cos²θ-1
より、
　cos2θ=9/16
△ＡＢＤにおいて、余弦定理より、
　BD²=AB²+AD²-2・AB・ACcos2θ
　　=4+9-2・2・3・9/16=25/4
BD＞0 より　BD=5/2
答え　AD=3, BD=5/2

(2)
　△ＡＥＢと△ＡＤＣは相似であるので、∠ＡＥＢ＝∠ＡＤＣ
よって、sin∠ＡＤＣ を求めることにする。
△ＡＤＣにおいて、余弦定理より、
　cos∠ＡＤＣ=(AD²+DC²-AC²)/(2・AD・DC)
　　=(9+2-8)/(2・3・√2) = 1/2√2
よって、
　sin∠ＡＤＣ=√(1-1/8)=√7/2√2
答え　√7/2√2

「算数・数学」の部屋に戻る