問題
横置き円柱に液体を貯めたとき 液深と容積の関係式を教えて下さい。
解答
底面の半径を r 、円柱の高さを h 、液の深さを d とし、その他の寸法を図のように決めます。
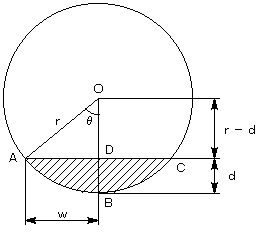
図の斜線部分の面積が求まれば、それに h を掛けると体積が求まりますので、斜線部分の面積を
求める問題として考えます。
斜線部分の面積をSとします。
(i) d≦r のとき
S=(扇形O−ABC)−△OAC
ここで、
θ=Cos-1{(r-d)/r}
w=√{r2-(r-d)2}=√(2rd-d2)
より、
(扇形O−ABC)=πr2×(2θ/2π)=r2Cos-1{(r-d)/r}
△OAC=w(r−d)=(r−d)√(2rd-d2)
よって、
S=r2Cos-1{(r−d)/r}−(r−d)√(2rd-d2)
「算数・数学」の部屋に戻る