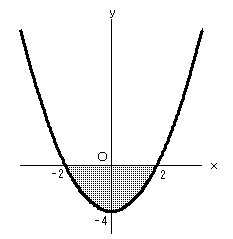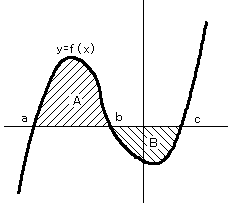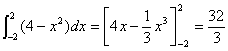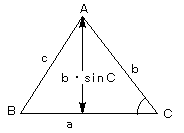ふじまみさんからの質問
２問あります。

問題１
　放物線　y＝ｘ²−４　とx軸で囲まれる図形の面積を表せ。

解答１
　これは、何をおいても、グラフが描けなければいけません。
　y＝ｘ²のグラフを描いて、それをｙ軸方向に−４、つまり下に ４ 動かしたのが
　y＝ｘ²−４ のグラフです。
　このときに重要なのが、ｘ軸との交点ですが、これは、
　　ｘ²−４＝０
　を解きます。交点は (-2, 0) と (2, 0) です。
　
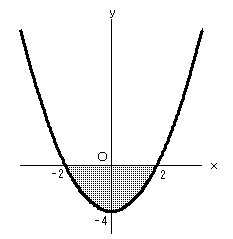
　さて、積分による面積の求め方ですが、下の図を見てください。
　
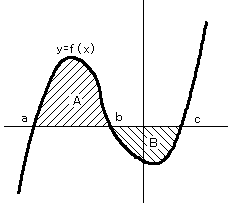
　この関数 y=f(x) を ａ〜ｃ の範囲で積分するとどうなるでしょう。
　ａ〜ｂ の部分（Ａ）は、グラフがｘ軸の上にありますから、積分値は正（＋）です。
　一方、ｂ〜ｃの部分（Ｂ）は、グラフがｘ軸の下にありますから、積分値は負（−）です。
　ａ〜ｃで積分すると、これらを合わせた値になりますから、正と負が相殺されます。
　もし、面積を求めるなら、Ａは正（＋）なのでそのまま、Ｂは符号を変えて積分しなければ
　なりません。つまり、面積Ｓは、
　　
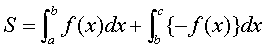
　となります。　

　さて、前置きが長くなりましたが、 ｙ＝ｘ²−４ で、ｘ軸と囲まれた部分は、ｘ軸の下にあるので、
このまま積分すると、値が負になってしまいます。
　そこで、−１を掛けて、　４−ｘ² を -2〜2 の範囲で積分します。
　
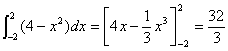
となります。途中の積分の計算は省略しています。


問題２
三角形ABCの３辺をa=BC　、b=CA　、c=ABで、内角をそのまま A,B,Cで表し、
三角形の面積をSで表すとき、次のうち正しいのはどれか？
　1；　S=1/2ab sinC
　2;　c sinB=b sinC
　3;　a sinB=b sinA
　4;　a=c sinB+b sinC
　5; c=a cosB+b cosA

解答２
　１．は三角形の面積の公式であるので、正しいです。
　　この公式の意味は、ａを底辺におくと、高さは、ｂsinＣになるためです。（ａとｂが逆でも可）
　
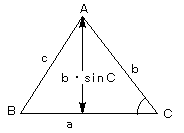
　２．は上の図で、ｂsinＣに当たる部分（底辺ａに対する高さ）を、ｃ と Ｂ を使うと、
　　ｃsinＢ となり、ともに同じ部分の長さを表しているので、正しいです。
　同じように考えると、ａsinＢはＣから対辺におろした垂線の長さ、ｂsinＡはＢから対辺に
　おろした垂線の長さなので、これらが常に等しいとは限らないので、３．は誤りです。
　４．は２．で考えた「高さ」を２つ足したもので、これがａに等しいとは言えないので誤りです。

　ちなみに、a=c cosB+b cosC なら正しいです。これを、第一余弦定理といいます。
　説明はこちらを見ていただくとして、同じ理由で、５．も正しいです。

「算数・数学」の部屋に戻る