問題
四角形ABCDにおいてAD//BC、AB=2、AD=3、cos∠ABC=1/5とする。
(1)Aから辺BCに下ろした垂線とBCとの交点をEとすると、BE=(ア)/(イ)であり、BD2=(ウ)/(エ)である。
(2)三角形ABDの外接円上に、BF=1となる点Fをとり、四角形ABFDを作る。
このとき、cos∠BFD=(オ)/(カ)であり、FD=(キ)、cos∠ABF=(ク)/(ケ)である。
解答
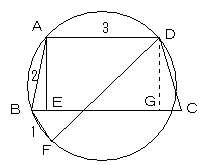
(1) BE=AB×cos∠ABC=2×1/5=2/5………(ア)/(イ)の答え
DからBCに垂線をおろし、その足をGとすると、EG=AD=3 である。
よって、BG=2/5+3=17/5
△ABEにおける三平方の定理より
AE2=AB2−BE2=96/25
GD=AE なので、
△BDGにおける三平方の定理より
BD2=BG2+GD2=(17/5)2+96/25=77/5………(ウ)/(エ)の答え
(2)AD//BC より、
∠ABC+∠BAD=180°
また、四角形ABFDは円に内接するので、
∠BAD+∠BFD=180°
よって、
∠ABC=∠BFD
なので、cos∠BFD=cos∠ABC=1/5………(オ)/(カ)の答え
△BFDにおける余弦定理より、
BD2=BF2+FD2−2BF・FDcos∠BFD
77/5=1+FD2−2FD/5
両辺5を掛けて整理すると、
5FD2−2FD−72=0
これを解いて、FD=(1±19)/5
FD>0より、 FD=4………(キ)の答え
cos∠ABF=t とおくと、cos∠ADF=cos(180°−∠ABF)=−t
△ABFと△AFDの双方から、余弦定理を使って、AF2 を表すと、
AF2=AB2+BF2−2AB・BFcos∠ABF
=4+1−2・2・1・t=5−4t
AF2=AD2+DF2−2AD・DFcos∠ADF
=9+16+2・3・4t=25+24t
よって、
5−4t=25+24t
これを解いて、
28t=−20
cos∠ABF=t=−5/7………(ク)/(ケ)の答え
算数・数学の部屋に戻る