問題
円Oに内接する四角形ABCDがあり、AB=4、AD=5、cos∠BAD=−1/5である。また対角線ACとBDは垂直に交わるとする。
このとき、BCと、四角形ABCDの面積を求めよ。
解答
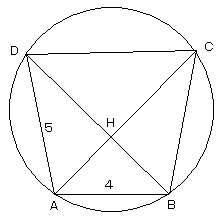
ACとBDの交点をHとします。
△ABDにおける余弦定理より、
BD2=AB2+AD2−2AB・ADcos∠BAD=49
より、
BD=7
また、sin∠BAD=2√6/5 より、
△ABDの面積は
△ABD=(AB・ADsin∠BAD)/2=4√6
BDを底辺にすると、AHが高さなので、
AH=4√6÷7×2=8√6/7
△ABHにおける三平方の定理より、
BH2=AB2−AH2=16−384/49=400/49
よって、
BH=20/7
同時に、
DH=7-20/7=29/7
△ADHと△BCHの相似より、
BC:AD=BH:AH
BC=AD・BH/AH
=25/2√6
同様に、
HC=DH・BH/AH
=145/14√6
AC=AH+HC=241√6/84
よって、四角形ABCDの面積Sは、
S=BD・AC/2
=241√6/24
「算数・数学」の部屋に戻る