問題
半径1の円に内接する四角形ABCDにおいて,AB=√3,∠ADC=75°,∠BCD=120°であるとき
(1)∠ADB,∠DACの大きさを求めよ。
(2)線分CD,ACの長さを求めよ。
解答
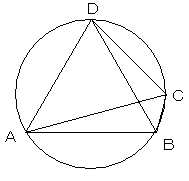
(1) △ABDにおける正弦定理より、
AB/sin∠ADB=2R
√3/sin∠ADB=2
sin∠ADB=√3/2
0°<∠ADB<75° より、
∠ADB=60°
円周角より、
∠ACB=∠ADB=60°
よって、
∠ACD=120°−60°=60°
△ACDの内角の和を考えると、
∠DAC=180°−∠ACD−∠ADC
=180°−60°−75°
=45°
(2)△ACDにおける正弦定理より、
CD=2R・sin∠DAC
=2・sin45°=√2
同じく
AC=2R・sin∠ADC
=2・sin75°
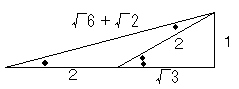
このような図を考えると(●1個が15°)、
sin75°=(√6+√2)/4
よって、
AC=(√6+√2)/2
「算数・数学」の部屋に戻る