問題
円に内接する四角形において4辺の長さa,b,c,d が与えられた時
その面積 S は
S=√(s-a)(s-b)(s-c)(s-d) 但しs=(a+b+c+d)/2
で表されることを証明せよ。
解答
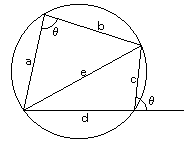
円に内接する四角形では、向かい合う角の和は180度であるので、
図のように角度θをおくことが出来る。
cos(180°-θ)=-cosθ
を考慮して、余弦定理の式を適用すると、
e2=a2+b2−2abcosθ
e2=c2+d2+2cdcosθ
より、
a2+b2−2abcosθ=c2+d2+2cdcosθ
cosθ=(a2+b2−c2−d2)/2(ab+cd)
sin2θ+cos2θ=1 より、
sin2θ=1−(a2+b2−c2−d2)2/4(ab+cd)2
={8abcd+2(a2b2+a2c2+a2d2+b2c2+b2d2+c2d2)-(a4+b4+c4+d4)}/4(ab+cd)2
四角形の面積Sは
S=(ab+cd)sinθ/2=(1/4)√{8abcd+2(a2b2+a2c2+a2d2+b2c2+b2d2+c2d2)-(a4+b4+c4+d4)}
一方、
(s-a)(s-b)(s-c)(s-d)=(a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d)/16
={8abcd+2(a2b2+a2c2+a2d2+b2c2+b2d2+c2d2)-(a4+b4+c4+d4)}/16
よって、
√(s-a)(s-b)(s-c)(s-d)=(1/4)√{8abcd+2(a2b2+a2c2+a2d2+b2c2+b2d2+c2d2)-(a4+b4+c4+d4)}
となり、√(s-a)(s-b)(s-c)(s-d) が面積と一致する。
算数・数学の部屋に戻る