問題
正三角形ABCを底面とする1辺の長さ4の正四面体ABCDがある。
ABを3:1に内分する点をEとし、BCの中点をFとする。AFとCEの交点をGとする。
底面ABCに垂直な直線をGに立てこの直線がADを延長した直線と交わる点をHとする。
(1)AGの長さを求めよ。
(2)∠AFH=θとするときcosθの値を求めよ。
解答
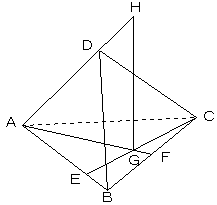
(1)
AF=2√3 であることを確認した上で、
メネラウスの定理より、
(AG/GF)(FC/CB)(BE/EA)=1
(AG/GF)(1/2)(1/3)=1
よって、
AG:GF=6:1
AG=AF×6/7=12√3/7
(2)
DからAF上に垂線を下ろした足をJとすると、
AJ:JF=2:1
なので、
AJ=4√3/3
よって、
AJ:AG=4√3/3:12√3/7=7:9
一方、
AD:AH=AJ:AG
より、
AH=AD×9/7=36/7
△AHGにおける三平方の定理より、
GH=12√6/7
また、FG=2√3/7 より、△FGHにおける三平方の定理より、
FH=2√219/7
よって、
cosθ=FG/FH=1/√73
算数・数学の部屋に戻る