問題
黄色の長方形(縦900、横1200)と赤い長方形(縦900、横200)が図左のように、重心を重ねて置かれています。

赤い長方形をこの位置から、反時計回りに15°、30°、45°回転したとき、
赤い長方形の4辺またはその延長線が、黄色い長方形の辺を切る位置を求めよ。
解答
まず、一般化してから求めます。
aratameさんからの質問1
問題
黄色の長方形(縦900、横1200)と赤い長方形(縦900、横200)が図左のように、重心を重ねて置かれています。

赤い長方形をこの位置から、反時計回りに15°、30°、45°回転したとき、
赤い長方形の4辺またはその延長線が、黄色い長方形の辺を切る位置を求めよ。
解答
まず、一般化してから求めます。
| 補題 縦2a、横2bの大きい長方形と、縦2c、横2dの小さい長方形があり、重心が重なっています。 小さい長方形を反時計回りにθ回転したとき、小さい長方形の4辺またはその延長線が、 大きい長方形の辺またはその延長線を切る位置を求めよ。 ただし 0°<θ<90°とする 点対称なので、どちらか一方で考えます。 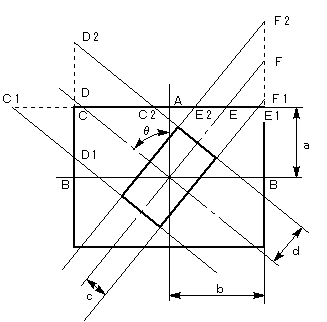 大きい長方形の横の辺の中点をA、縦の辺の中点をBとします。 小さい長方形の縦の辺が大きい長方形の横の辺を切る位置をC1、C2 とし、その中点をCとします。 小さい長方形の縦の辺が大きい長方形の縦の辺を切る位置をD1、D2 とし、その中点をDとします。 小さい長方形の横の辺が大きい長方形の横の辺を切る位置をE1、E2 とし、その中点をEとします。 小さい長方形の横の辺が大きい長方形の縦の辺を切る位置をF1、F2 とし、その中点をFとします。 AC=a・tanθ、 CC1=CC2=d/cosθ より、 AC1=a・tanθ+d/cosθ、 AC2=a・tanθ−d/cosθ BD=b/tanθ、 DD1=DD2=d/sinθ より、 BD1=b/tanθ−d/sinθ、 BD2=b/tanθ+d/sinθ AE=a/tanθ、 EE1=EE2=c/sinθ より、 AE1=a/tanθ+c/sinθ、 AE2=a/tanθ−c/sinθ BF=b・tanθ、 FF1=FF2=c/cosθ より、 BF1=b・tanθ−c/cosθ、 BF2=b・tanθ+c/cosθ |
この問題の場合、
a=450、b=600、c=450、d=100 である。
| θ=15°の時 sin15°=(√6−√2)/4 cos15°=(√6+√2)/4 tan15°=(√6−√2)/(√6+√2) =2−√3 を使います。  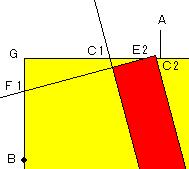 |
GC1=GA−AC1 =b−(a・tanθ+d/cosθ) =600−(450tan15°+100/cos15°) =450√3+100√2−300−100√6 ≒375.9 GC2=GA−AC2 =b−(a・tanθ−d/cosθ) =600−(450tan15°−100/cos15°) =450√3−100√2−300+100√6 ≒583.0 AE2=−a/tanθ+c/sinθ ※E2がAより左にあるので、上の解説とは、 符号が逆になります GE2=b−(−a/tanθ+c/sinθ) =600+450/tan15°−450/sin15° =600+450(2+√3)−450(√6+√2) =1500+450√3−450√6−450√2 ≒540.8 BF1=−b・tanθ+c/cosθ ※同様に符号が逆になります。 GF1=a−(−b・tanθ+c/cosθ) =450+600tan15°−450/cos15° =1650+450√2−600√3−450√6 ≒144.9 |
| θ=30°の時 sin30°=1/2 cos30°=√3/2 tan30°=√3/3 を使います。  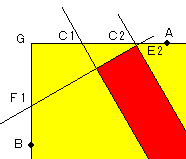 |
GC1=GA−AC1 =b−(a・tanθ+d/cosθ) =600−(450tan30°+100/cos30°) =600−650√3/3 ≒224.7 GC2=GA−AC2 =b−(a・tanθ−d/cosθ) =600−(450tan30°−100/cos30°) =600−250√3/3 ≒455.7 AE2=−a/tanθ+c/sinθ ※同様に符号が逆になります。 GE2=b−(−a/tanθ+c/sinθ) =600+450/tan30°−450/sin30° =600+450√3−900 =450√3−300 ≒479.4 BF1=−b・tanθ+c/cosθ ※同様に符号が逆になります。 GF1=a−(−b・tanθ+c/cosθ) =450+600tan30°−450/cos30° =450−100√3 ≒276.8 |
| θ=45°の時 sin45°=√2/2 cos45°=√2/2 tan45°=1 を使います。  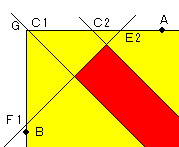 |
GC1=GA−AC1 =b−(a・tanθ+d/cosθ) =600−(450tan45°+100/cos45°) =150−100√2 ≒8.579 GC2=GA−AC2 =b−(a・tanθ−d/cosθ) =600−(450tan45°−100/cos45°) =150+100√2 ≒291.4 AE2=−a/tanθ+c/sinθ ※同様に符号が逆になります。 GE2=b−(−a/tanθ+c/sinθ) =600+450/tan45°−450/sin45° =1050−450√2 ≒413.6 BF1=−b・tanθ+c/cosθ ※同様に符号が逆になります。 GF1=a−(−b・tanθ+c/cosθ) =450+600tan45°−450/cos45° =1050−450√2 ≒413.6 |