問題1 sinθ=−3/5 のとき、θは第何象限の角か。
また、そのときのcosθ、tanθの値を求めよ。
問題2 sinθ=αのとき、sin4θ+cos4θをαの式で表せ。
問題3 sinθ+cosθ=1/√3のとき、tanθ+1/tanθの値を求めよ。
問題4 1+1/tan2θ=1/sin2θを証明せよ。
(解答)
まずは、座標上での角度の表し方と、象限について、基礎的なことを確認しておきます。
TANEさんからの質問2
問題1 sinθ=−3/5 のとき、θは第何象限の角か。
また、そのときのcosθ、tanθの値を求めよ。
問題2 sinθ=αのとき、sin4θ+cos4θをαの式で表せ。
問題3 sinθ+cosθ=1/√3のとき、tanθ+1/tanθの値を求めよ。
問題4 1+1/tan2θ=1/sin2θを証明せよ。
(解答)
まずは、座標上での角度の表し方と、象限について、基礎的なことを確認しておきます。

通常は、下の図のように、単位円(原点を中心として、半径1の円)に対して、角度を決めますが、
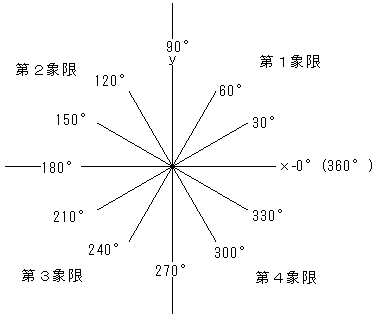
x軸方向を0°。そこから、原点を中心に角度を決めます。
また、その延長として、360°を超える角度や、負の角度も決めることが出来ます。
座標平面が、x軸、y軸で区切られる4つの部分を、角度の方向の順に第1象限、第2象限、第3象限
第4象限といいます。つまり、30°, 60°は第1象限の角、120°,
150°は第2象限の角、210°, 240°
は第3象限の角、300°, 330°は第4象限の角、ということになります。
座標軸上の角度(0°, 90°, 180°, 270°など)は、どの象限にも属しません。
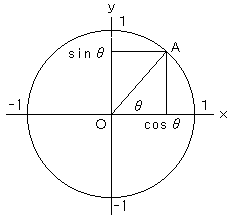
さて、図のように単位円と角度θの半径(動径という)を取ると、単位円上の点Aのx座標が cosθ、y座標
が sinθ ということが出来ます。
これを拡張して、90°以上の角度についても、sin、cos
を定義することが出来ます。つまり、
| θ | sinθ | cosθ | tanθ(=sinθ/cosθ) |
| 第1象限 | + | + | + |
| 第2象限 | + | − | − |
| 第3象限 | − | − | + |
| 第4象限 | − | + | − |
のようになります。
では、解答です。
問題1
sinθ=-3/5 となる角度は、θが∠XOAまたは∠XOBに一致するときである。
つまり、第3象限、または第4象限。
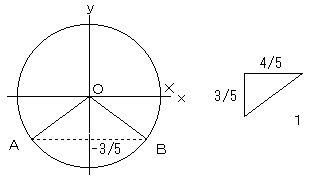
θ=∠XOA(第3象限) のとき cosθ=-4/5、tanθ=sinθ/cosθ=3/4
θ=∠XOB(第4象限) のとき cosθ=4/5、tanθ=sinθ/cosθ=-3/4
図右側の三角形を参照。
問題2
公式 sin2θ+cos2θ=1
を知っていればすぐ解けますが、まだ習っていないならば、下図の?の部分が
cosθに
なるので、cos2θ=1−α2 と求めることが出来ます。今後必要なら、この方法でこの
公式を証明してください。
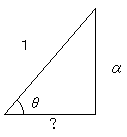
以上より、
sin4θ+cos4θ=(sin2θ)2+(cos2θ)2
=α4+(1−α2)2=2α4−2α2+1
問題3
公式 sin2θ+cos2θ=1 は知っているものとして説明します。
求める式 tanθ+1/tanθ を変形すると
tanθ+1/tanθ=sinθ/cosθ+cosθ/sinθ
=(sin2θ+cos2)/sinθcosθ
=1/sinθcosθ
一方、sinθ+cosθ=1/√3 の両辺を2乗して
sin2θ+2sinθcosθ+cos2=1/3
1+2sinθcosθ=1/3
2sinθcosθ=1/3−1=−2/3
sinθcosθ=−1/3
よって、
tanθ+1/tanθ=−3
問題4
tanθが定義されているので、sinθ≠0 としても良い。
公式 sin2θ+cos2θ=1 の両辺を sin2θ で割って
1+1/tan2θ=1/sin2θ
が得られる。
「算数・数学の部屋」に戻る