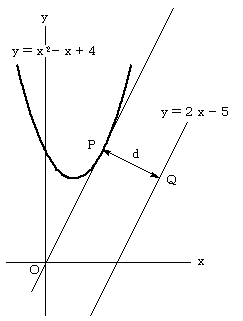TANEさんからの質問8
問題
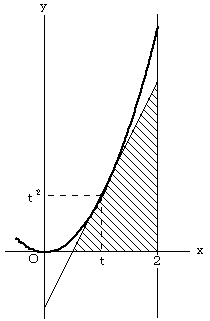
(1) y=x2で表される放物線をCとする。
0≦t≦2と し、放物線C上の点(t、t2)における接線、直線x=2、 およびx軸により囲まれる部分
の面積をF(x)と表すことにする。
このとき、
F(x)=(ア)t3−(イ)t2+(ウ)t
よって、
t=(エ)
のとき、F (x)は最大値(オ)をとる。
(2) 点Pは曲線y=x2−2x+4の上を動き、点Qは直線y=2x−5上を動くものとすると、
線分PQの長さの最小値は(カ)であ る。
また、PQの長さが(カ)となるのは、Pの座標が(キ、ク)でQの座標が(ケ、コ)のときである。
(3) sinθ+7cosθが最大となるのは、tanθ=(
サ) のときで、その最大値は(シ)である。
解答
(1)
 |
g(x)=x2
とおくと、
g’(x)=2x
よって、点(t,t2)における接線の式は、
y=2t(x−t)+t2 ・・・(i)
(i) にx=2を代入して、
y=2t(2−t)+t2=4t−t2
より、(i) と直線x=2との交点は、
(2,4t−t2)
また、(i) にy=0を代入して、
0=2t(x−t)+t2
t=0のときは、面積は0となるのでt≠0も条件下でこれを解くと、
x=t/2
よって、面積は
F(x)=(2−t/2)(4t−t2)/2
=t3/4−2t2+4t ・・・(ア)=1/4、(イ)=2、(ウ)=4
F(x)をxで微分して、
F’(x)=3t2/4−4t+4
F’(x)=0となるのは、x=4/3、4
0≦x≦2 の範囲で増減表を書くと
| x |
0 |
|
4/3 |
|
2 |
| F’(x) |
+ |
+ |
0 |
− |
− |
| F(x) |
0 |
増 |
64/27 |
減 |
2 |
よって、x=4/3 のとき、F(x)は最大値
64/27 をとる。
(エ)=4/3、(オ)=64/27 |
(2)
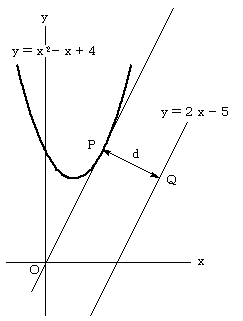 |
直線 y=2x−5 と平行な直線を、図のように
曲線 y=x2−2x+4 と接するように引いたとき、そのときの
接点をP、Pから直線 y=2x−5 に下ろした垂線の足をQとするとき、
線分PQの長さdは最小になる。
y=x2−2x+4
を微分して、
y’=2x−2
y’=2 となるのは、x=2のとき。
よって、点Pを(2,4)にとる。・・・(キ、ク)
直線PQの傾きは、−1/2なので、直線PQの式は、
y=−(x−2)/2+4
y=−x/2+5
y=2x−5 との交点を求めると、Q:(4,3)・・・(ケ、コ)
よって、PQの長さは、
√{(4−2)2+(3−4)2}=√5・・・(カ) |
別解
この問題では、点Qの座標まで答えさせているので、上記のように解いたが、
PQの長さだけをきく問題であれば、y=2x−5
を 2x−y−5=0 と変形して、
点と直線までの距離の公式より、
PQ=|2・2−4−5|/√(22+12)=√5・・・(カ)
としてもよい。
(3)
f(θ)=sinθ+7cosθ とおく。
sinφ=7/√50、 cosφ=1/√50 となるような角度φをとると、
f(θ)=√50(sinθcos φ+cosθsinφ)
=√50sin(θ+φ)
とかける。
sin(θ+φ)=1 のとき、f(θ)は最大値
√50 となる。
つまり θ+φ=π/2+2nπ (nは整数)
のときであるが、このとき、
θ=π/2−φ+2nπ
tanθ=tan(π/2−φ)=cotφ=cosφ/sinφ=1/7
よって、tanθ=1/7 のとき、最大値 √50 をとる。・・・(サ)(シ)
ただし、tanθ=1/7 のとき、必ずしも最大にはならないことは、念頭に置いておく必要がある。
この問題では、「最大となる」ことを前提に話をしているので一応これでも良いが、最小値もまた、
tanθ=1/7のときに現れる。
「算数・数学」の部屋に戻る