問題
半径4の円に内接する四角形ABCDがあり、AB=5、∠ABC=60°とするとき、四角形ABCDの面積の最大値を求めよ。
解答
条件により、3点A,B,Cの位置は決まります。
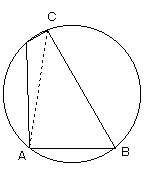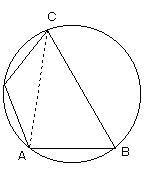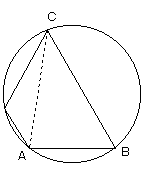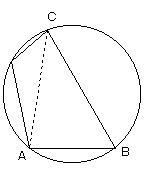
正弦定理より、sin∠ACB=AB/2R=5/8 (Rは半径)
また、cos∠ACB=√{1-(5/8)2}=(√39)/8
加法定理より、
sin∠CAB=sin(120°−∠ACB)=
=sin120°cos∠ACB−cos120°sin∠ACB
=(√3/2)(√39)/8−(-1/2)(5/8)
=(3√13+5)/16
正弦定理より、AC=2R・sin∠ABC=4√3
よって、
△ABC=(1/2)AB・AC・sin∠CAB
=(1/2)・5・4√3・(3√13+5)/16
=(25√3+15√39)/8 ・・・(一定)
一方、△ACDは、点Dが直線ACからもっとも離れたときに面積最大であり、
それは、AD=CDとなるときである。
∠ADC=180°−∠ABC=120°
であるので、AD=CDとなるのは、∠DAC=∠DCA=30°のとき。つまり、
AC=4√3
より、ACを底辺としたときの△ACDの高さは
AC/2√3=2
よって、△ACD=4√3×2÷2=4√3
以上より、四角形ABCDの面積の最大値は、
(25√3+15√39)/8+4√3
算数・数学の部屋に戻る