半熟プログラマーさんからの質問

問題

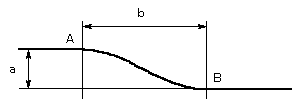
図の点Ａと点Ｂは高さの差がａ、水平距離がｂであり、その間の曲線は、sin カーブになっている。
（点Ａ、点Ｂで、極大、極小になっていて、1/2 波長の波）
このとき、点Ａからｘ離れた地点での点Ｂからの高さを求めよ。

解答
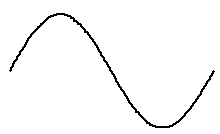
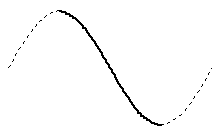
点Ａと点Ｂの間は、下左図の sin 曲線１波長分の半分（下右図）を使って、なめらかに結ばれている。
　　

問題の図に下のような座標軸を取ると、この曲線は、振幅 a/2, 波長 2b の sin 曲線になっている。

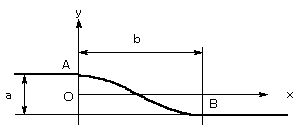
さらに極大点からグラフが始まっているので、（位相が９０°ずれているので） cos のグラフとして
考えた方がわかりやすい。
一般に振幅 α, 波長 λ のsin 曲線の式は
　y =α sin(２πｘ/λ) の式で表される。（π rad ＝180°)
α=a/2, λ = 2b として、cos で考えると、
　y = (a/2) cos(２πｘ/２ｂ) = (a/2) cos(πｘ/ｂ)
さらに、原点は点Ｂよりも a/2 上方にあるので、
　y = (a/2){1 + cos(πｘ/ｂ)}
と表せる。

「算数・数学」の部屋に戻る