質問・問題に答えるコーナー(平面図形に関する問題)

分野	質問された方	掲載日	質問内容　答えは質問者のお名前をクリック
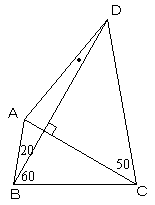
平面図形	幹さん	2000/11/11	一辺が８ｃｍ．１２ｃｍの長方形があります。 １２cmの中点に向かい、折り返します。 この時、折り返した斜辺の長さを求めなさい。
平面図形	里奈さん２	2001/01/25	AB＝ACである三角形ABCの辺BC上に２点D、Eを BD＝DE＝ECとなるようにとり、 またDAの延長線 と、CからEAに平行に引いた直線との交点をFとするとき AF＝AEとなることを証明しなさい。
平面図形	里奈さん３	2001/02/13	次の図でAB＝５ｃｍ、BC＝８ｃｍ、CA＝７ｃｍ、ABとQPが平行、 ∠ABR＝∠RBPであるときに、BPの長さを求めなさい。
作図	里奈さん４	2001/03/08	四角形ＡＢＣＤの頂点Ａを通り、四角形の面積を２等分する直線を引きなさい。
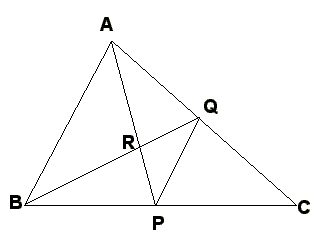
平面図形	里奈さん４	2001/03/08	下図でＡＢ＝５ｃｍ、ＢＣ＝８ｃｍ、ＣＡ＝７ｃｍ、ＡＢ//ＱＰ、∠ＢＡＰ＝∠ＢＣＡ であるときに（∠ＡＢＲ＝∠ＲＢＰとは限らない）、 ＰＲの長さがＡＲの長さの３９/６４倍となることを証明しなさい。
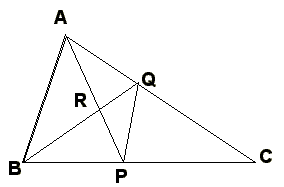
円の接線の作図	aina さん	2001/06/06	大きさの違う円に共通する２本の接線を２通りの方法で作図します。 接線の引き方を教えてください。
円周角	さちさん	2001/07/19	(1)正９角形の、３つの頂点を結んで、三角形を作るとき、鈍角三角形は何個できるか。 (2)また、３つの内角の大きさがそれぞれ２０°、４０°、１２０°になる三角形は何個できるか。
直角三角形	みゅゥさん３	2001/08/15	（１）∠ＢＡＣ＝９０°の直角三角形ＡＢＣがあり、ＡからＢＣにおろした垂線の足をＨとする。 　i) △ＡＨＣの外接円を描くことにより、ＢＡ2＝ＢＨ・ＢＣを方べきの定理を用い証明せよ。 　ii) 適当な円を描くことにより、ＡＨ2＝ＢＨ・ＨＣを方べきの定理を用い証明せよ。 （２） 　i) ユークリッドの定理を用いて三平方の定理ＢＣ2＝ＡＢ2＋ＣＡ2を証明せよ。 　ii) ユークリッドの定理ＡＢ・ＡＣ＝ＢＣ・ＡＨ（＝２・三角形ＡＢＣ）を利用して、 　　　１/ＡＢ2＋１/ＣＡ2＝１/ＡＨ2 　　を証明せよ。
三角不等式	めかさん２	2001/08/16	△ＡＢＣ内の一点をＯとするとき、 　ＡＢ＋ＢＣ＋ＣＡ＞ＯＡ＋ＯＢ＋ＯＣ＞（ＡＢ＋ＢＣ＋ＣＡ）/2 となることを証明せよ。
平面図形	みゅゥさん４	2001/08/18	∠ＢＡＣ＝９０°の直角３角形ＡＢＣの内接円Ｉを描く。 ＡＢ＝ｃ、ＢＣ＝ａ、ＣＡ＝ｂ、内接円Ｉの半径＝ｒとするとき、 　i) 円Ｉと２辺ＡＢ、ＣＡとの接点をそれぞれＴ，Ｓとするとき、ＡＴ＝ＡＳ＝ｒとして、ｒをａ、ｂ、ｃで表しなさい。 　ii) 三角形ＡＢＣの面積を２通りに表すことにより、ｒをａ、ｂ、ｃを用いて表せ。 　iii) i)、ii) で導いた等式を利用して、ａ2＝ｂ2＋ｃ2（三平方の定理）を証明せよ。
方べきの定理	みゅゥさん６	2001/08/21	円Ｏの円周外の１点Ｐから接線ＰＡ、ＰＢをひき、ＰＯと弦ＡＢとの交点をＭとする。 また、点Ｐより円Ｏへ割線をひき、円周との交点をＱ，Ｒとする。 このとき、４点Ｏ、Ｍ、Ｑ、Ｒは同一円上にあることを証明せよ。
平面図形	Toshi さん１	2001/08/27	問題１ △ＡＢＣにおいて、ＡＢ＝３，ＢＣ＝２，ＣＡ＝４とする。 △ＡＢＣの内心をＰとし、内接円とＢＣの接点をＱ、Ｑから直線ＡＰに垂線を引き、 ＡＣとの交点をＲとする。このとき比ＡＲ：ＲＣを求めよ。 問題２ Ｏを原点とする座標平面上に点Ａ(0,90)，点Ｂ(0,40)がある。 そしてX軸上の正の部分に点Ｐをおいて角ＡＰＢが最大になるようにするとき、 ＯＰの長さを求めなさい。
内心・外心	みゅゥさん７	2001/08/29	鋭角三角形ＡＢＣのＡＢ＝ｃ、ＢＣ＝ａ、ＣＡ＝ｂとするとき、鋭角三角形ＡＢＣの内心Ｉから、 鋭角三角形の外接円Ｏへの方べきをＰとすると、Ｐ＝ａｂｃ/(ａ＋ｂ＋ｃ) となることを証明せよ。
三角不等式	めかさん３	2001/08/30	三角形の二角が等しくないとき、大きい角に対する辺は小さい角に対する辺よりも大きい事を証明してください。
平面図形	mouretuさん	2001/09/14	同じ半径ｒであり、異なる中心Ｏ１、Ｏ２、Ｏ３をもつ３つの円がある。 これらが点Ｎにより交わるとき、それぞれもう1方の交点Ａ、Ｂ，Ｃを通る円を描いた。 このときの円の半径を求めよ。
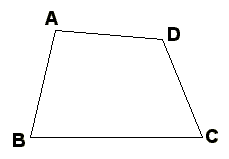
台形の２等分	たーさん	2000/11/13	ある台形の面積を２等分する場合、 どうすれば、求められるのでしょうか？ 条件．上底、下底に平行に分割する。
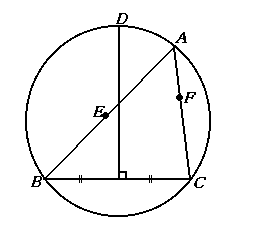円周角	Toshi さん３	2001/10/18	△ABCの外接円と、辺BCの垂直二等分線との交点Dを、 図のように点Aと同じ側に取る。 辺AB、AC上に点E、Fを4点A、D、E、Fが 同一円周上にあるように取るとき、 BE=CFを証明しなさい。
平面図形	いちろーさん１	2001/10/28	一辺の長さ２の正三角形ABCの辺AB,BC,CA上にそれぞれ点 P,Q,R を 　AP=BQ=CR≦１ となるようにとる。△PQRの面積が△ABCの面積の１/２倍となるときのAPの長さをもとめよ。
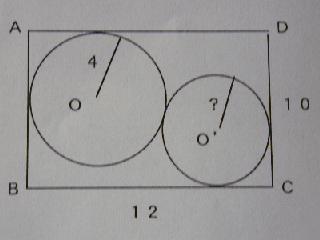三平方の定理	里奈さん７	2001/11/22	図において、円Ｏと円Ｏ’は互いに外接し、それぞれ長方形の２辺と接している。 長方形ＡＢＣＤにおいて、ＡＢ＝ＣＤ＝１０、ＢＣ＝ＡＤ＝12、円Ｏの半径を４とするとき、 円Ｏ’の半径を求めよ。
平面図形	トモさん１	2001/12/07	縦6ｃｍ、横8ｃｍの長方形の対角線と長方形の縦、横に接する２つの円を描いた。 円の中心を各O,O’とする。また、対角線に接する点をＰ，Ｑとする。 (1)　線分Ｐ，Ｑの長さは何ｃｍか (2)　線分Ｏ，Ｏ‘の長さは何ｃｍか
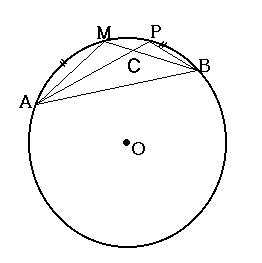平面図形	Toshi さん５	2001/12/16	円Ｏの弧ABの中点をM、弧AB上のM以外の点Pをとる。 このとき、ＡＰ＋ＢＰ＜ＡＭ＋ＭＢを示しなさい。
平面図形	miumiuさん１	2001/12/19	どの３点も一直線上にない、４点ABCDがあり、それぞれの２点を結ぶ直線は６本ひける。 その交点は何個できるか？ ただし、どの２直線も平行でないとする。
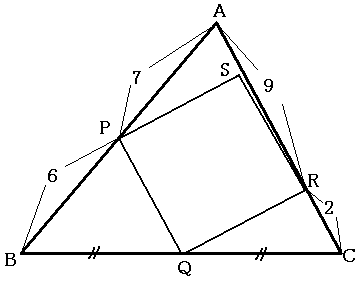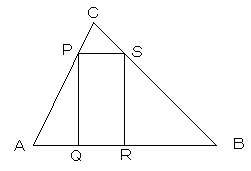
平面図形	カズさん１	2001/12/23	図のように三角形ＡＢＣの内部に正方形ＰＱＲＳが3点Ｐ、Ｑ、Ｒで接していて、ＢＱ＝ＱＣです。 このとき、正方形ＰＱＲＳの面積を求めなさい。
平面図形	たかさん１	2002/01/12	半径ｒの扇形ＯＡＢがある。 角ＢＯＡ＝90度で、AをＯに重なるように折りかえした時の折り目をＣＤとする。 1　ＣＤの長さを求めよ。 2　ＢＯＣの周の長さを求めよ。 3　ＢＯＣの面積を求めよ。
平面図形	Toshiさん６	2002/02/05	△ABCの頂点Aにおける外角の２等分線が、 辺BCの延長および外接円とそれぞれD、Eで交わるとすると (1) AB・AC=AD・AE (2) AD2=BD・CD-AB・AC であることを証明せよ。
平面図形	チャコさん１	2002/02/04	与えられた正方形と面積の等しい正三角形を作図する。
平面図形	山本達也さん１	2002/02/23	n角形の対角線の交点の数は？
平面図形	華暢さん１	2002/02/24	五角形ABCDEにおいて 　角A＝90度 　角B＋角D＝270度 　角C＋角E＝180度 　AB＝BC＝CD＝DE＝EA＝2cm 　この時、五角形ABCDEの面積を求めよ。
平面図形	hiroyaさん１	2002/03/29	△ＡＢＣがあり、４点Ｐ，Ｑ，Ｒ，Ｓをそれぞれ、ＡＣ上、ＡＢ上、ＡＢ上、ＢＣ上にとり、 四角形ＰＱＲＳが 　ＰＱ＝２ＰＳ を満たす長方形になるように作図せよ。
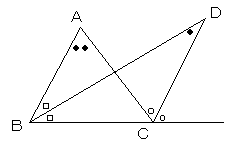
平面図形	keiichiro さん１	2002/03/28	△ＡＢＣにおいて、∠Ｂの二等分線と、∠Ｃの外角の二等分線の交点をＤとするとき、 　∠ＢＡＣ＝２∠ＢＤＣ であることを証明せよ。
平面図形	かわうそさん１	2002/03/07	円の中に内接している正五角形があってその円の半径をｒとして その五角形の１辺の長さをｒを使って表せ。
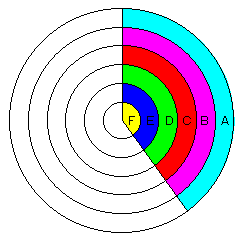平面図形	里奈さん１１	2002/02/25	図のように中心を共有する6つの円がある。 各円の半径の差は全て等しく、また円Fの半径とも等しいとする。 A、B、C・・・はそれぞれの部分 の面積を表している。 このとき、次の式の答えをAからFを使って表しなさい。 1）D+E+F= 2）A+D-B= 3）C×E-A-B= 4）（A+B）÷（E+F）= 5）（2A+B）÷（E+F）= 6）（（D+F）×　C+B　）÷E
平面図形	やすさん１	2002/04/26	ユークリッドの定理5「二等辺三角形の底角は等しい」、定理16「三角形においてある角の外角は他の内角より大きい」を用いて （1）定理「三角形ＡＢＣにおいて、ＢＣ＞ＡＣならば∠Ａ＞∠Ｂ」の証明 （2）上の逆の証明 （3）定理「三角形の2辺の長さの和は、他の1辺の長さより大きい」の証明 この3つの証明を教えてください。
平面図形	T兄弟さん１	2002/06/30	図において、AC⊥BD です。このとき、∠ＡＤＢ を求めよ。 ※図の数値の単位は°です。

算数・数学の部屋に戻る