たーさんからの質問１

問題
ある台形の面積を２等分する場合、 どうすれば、求められるのでしょうか？
条件．上底、下底に平行に分割する。

解答

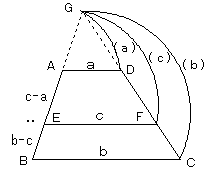
　上図のように、上底をａ、下底をｂとし、上底・下底に平行な直線で、この台形を２つに分けたときの
切り口の長さをｃとします。
　このとき、２つに分けられた台形の上底側の部分と下底側の部分の高さの比は、
　　ｃ−ａ：ｂ−ｃ
になります。
　２つの台形の面積が等しくなるには、
　　（ａ＋ｃ）×（ｃ−ａ）＝（ｂ＋ｃ）×（ｂ−ｃ）
　　ｃ²−ａ²＝ｂ²−ｃ²
　　２ｃ²＝ｂ²＋ａ²　・・・(a)
　ｃ＞０より、切り口の長さｃが
　　
となるような位置で、切れば良い。

別解
　上記の (a) の式の導出は、以下のようにしても出来ます。
　図において、△ＧＡＤ、△ＧＥＦ、△ＧＢＣは相似で、相似比は　ａ：ｃ：ｂ
　台形ＡＥＦＤ と 台形ＥＢＣＦ の面積が等しいことから、
　　△ＧＥＦ−△ＧＡＤ＝△ＧＢＣ−△ＧＥＦ
　面積比は、相似比の２乗に相当するから
　　ｃ²−ａ²＝ｂ²−ｃ²
　よって、
　　２ｃ²＝ｂ²＋ａ²　・・・(a)

　以下同様。


算数・数学の部屋に戻る