ある国のある州には冗談湖と言う1周6kmの湖がある。
ある年のある補習校のあるクラスが冗談湖のほとりでキャンプをした。
その生徒とその両親、とびいり参加した某先生とそのだんなも含めて総勢38名であった。
YSさんがきむたくを追いかけて いってなかなか帰ってこないので、残りの37名でボートに乗ることにした。
貸し ボート屋さんには2人乗りと3人乗りの2種類のボートがあり、料金はそれぞれ1時間当たり4ドル、5ドルである。
2種類のボートを何そうか借りて、全員が定員どお りに乗ったところ、1時間の料金は全部で69ドルとなった。
借りたボートは2人乗 り、3人乗りそれぞれ何そうあったか???
解答1 その1(鶴亀算による方法)
最初の3,4行の状況説明は、ほとんど問題に関係ありません。(必要なのは37人という人数だけ)
例えば、2人乗りをできるだけ多く使う方法は、
2人乗り 17そう、 3人乗り 1そう
で、このとき料金は、
17×4+1×5=73 (ドル)
2人乗り3そうの6人を、3人乗り2そうに置き換えると、
(3×4=)12ドルが、(2×5=)10ドルになるので、2ドル減る。
73ドルを69ドルにするには、4ドル減らさないといけないので、このような置き換えを2回行う。
結果、2人乗りは、6そう減って11そう、3人乗りは、4そう増えて5そうとなる。
答え:2人乗り11そう、3人乗り5そう
解答1 その2(方程式による方法)
2人乗りをxそう、3人乗りをyそう借りたとする。
人数の条件より
2x+3y=37 ・・・ (1)
料金の条件より
4x+5y=69 ・・・ (2)
これを解いて、x=11,y=5
答え:2人乗り11そう、3人乗り5そう
問題2
四角形ABCDの頂点Aを通り、四角形の面積を2等分する直線を引きなさい。
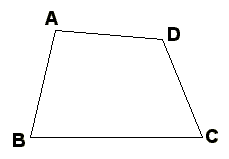
解答2
図のように、△ACDを△ACEに、等積変形すると、
四角形ABCDと△ABEの面積は等しくなり、BEの中点Mと点Aを結ぶ線を引けばよい。

問題3
下図でAB=5cm、BC=8cm、CA=7cm、AB//QP、∠BAP=∠BCA
であるときに(∠ABR=∠RBPとは限らない)、
PRの長さがARの長さの39/64倍となることを証明しなさい。
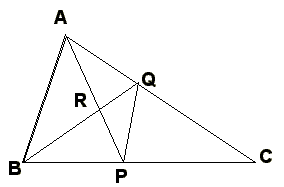
解答3

∠BAP=∠BCA、∠ABC=∠PBA より、△ABCと△PBAは相似である。
相似比は、8:5であるので、BP、APの長さは、上図のように、
BP=25/8、AP=35/8
と決まる。
また、PC=8−25/8=39/8

一方、AB//QPより、△ABCと△QPCも相似であり、相似比は、64:39 である。
また、△ABRと△PQRも相似であるので、
AR:PR=AB:PQ
これは、△ABCと△QPCの相似比と同じ64:39であるので、
AR:PR=64:39
以上より、PRの長さはARの長さの39/64倍である。