問題
どの3点も一直線上にない、4点ABCDがあり、それぞれの2点を結ぶ直線は6本ひける。
その交点は何個できるか?
ただし、どの2直線も平行でないとする。
解答
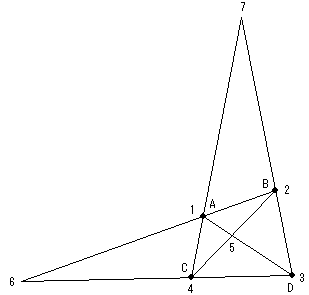
図から、明らかに7個なのですが、計算で求めてみます。
まず、2点を結ぶ直線が6本ひけるというのは、
A,B,C,D の中から 2点を選べば、それぞれ異なる直線が引けるので、
4×3÷2=6
です。
miumiu さんからの質問1
問題
どの3点も一直線上にない、4点ABCDがあり、それぞれの2点を結ぶ直線は6本ひける。
その交点は何個できるか?
ただし、どの2直線も平行でないとする。
解答

図から、明らかに7個なのですが、計算で求めてみます。
まず、2点を結ぶ直線が6本ひけるというのは、
A,B,C,D の中から 2点を選べば、それぞれ異なる直線が引けるので、
4×3÷2=6
です。
| これは、組み合わせという考え方で、まず、A,B,C,D
4個の文字から2個を選び、 並べる並べ方を考えます。 1個目に選ぶのは、A,B,C,D の4通り、2個目に選ぶのは、最初に選ばなかった 3個のうちの一つなので、3通りで、合計4×3=12通りです。つまり AB AC AD BA BC BD CA CB CD DA DB DC の12通りです。 これを、4個から2個選ぶときの順列といい、4P2 と書きます。4P2=12 です。 このうち、AB と BA、AC と CA など、並び順が違うだけで、中身は同じものが、 それぞれ2組ずつあります。この問題の場合、直線AB と 直線BA は同じ直線なので、 これらは1つとして数えます。すると、直線の数は 12÷2=6 となります。これを、4個から2個選ぶときの組み合わせといい、4C2 と書きます。4C2=6です。 一般に、n個からr個を選ぶ順列は nPr=n(n-1)(n-2)・・・(n-r+1)=n!/(n-r)! ここで n! は n の階乗といって、「1からnまでの整数をすべて掛けた数」です。 2!=1×2=2 3!=1×2×3=6 5!=1×2×3×4×5=120 また、n個からr個を選ぶ組み合わせは nCr=nPr/r!=n!/(n-r)!r! と書けます。 |
さて、いよいよ交点の数ですが、交点は平行でない2直線につき1個存在しますから、
上の、組み合わせの考えでいうと、「6本から2本選ぶ組み合わせ」になり、
6×5÷2=15
15個あるはずです。
ところが、この問題の場合、3本の直線が1点で交わるところがあります。
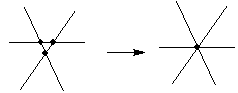
そうすると、図のように3個の点が1個になり、2個減ることになります。
こういう点が A,B,C,D の4カ所ありますから、8個減って、
15−8=7
7個となります。
答え 7個
算数・数学の部屋に戻る