問題
円の中に内接している正五角形があってその円の半径をrとして
その五角形の1辺の長さをrを使って表せ。
解答
五角形の面積から一部引用しています。
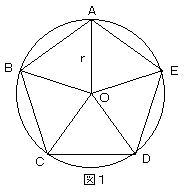
図2の△OABのにおいて、ABが求める長さです。

OBを底辺とすれば、高さは、図3のAHとなる。
ここで、図3の△AFOは、∠F=∠O=72°の二等辺三角形である。
図4のように、∠Oの二等分線OGを引くと、△AFOと△OGFは相似となる。
図4の●1つで36°を表す。
△OGFを抜き出したのが図5である。
△AFOと△OGFの辺の比より、
r:x=x:(r−x)
よって、
x2=r(r−x)
x2+rxーr2=0
x>0の範囲でxについて解くと
x=(−r+r√5)/2=r×(√5−1)/2
すると、
FH=HO=r×(√5−1)/4
となり、△AHFにおける三平方の定理より、
AH2=AF2−FH2=r2{1−(3−√5)/8}
=(5+√5)r2/8
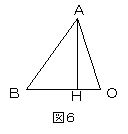
一方、図6において、
BH=BO−HO=r−(√5−1)r/4
=(5−√5)r/4
BH2=(30−10√5)r2/16=(15−5√5)r2/8
△ABHにおける三平方の定理より、
AB2=AH2+BH2=r2{(5+√5)+(15−5√5)}/8
=(20−4√5)r2/8
=(5-√5)r2/2
よって、
算数・数学の部屋に戻る