問題
(1)正9角形の、3つの頂点を結んで、三角形を作るとき、鈍角三角形は何個できるか。
(2)また、3つの内角の大きさがそれぞれ20°、40°、120°になる三角形は何個できるか。
解答
まず、円周角というものについて説明します。

上図において、円周上の2点A、Bと円の中心Oとで作る角(∠AOB)を中心角といいます。
一方、円周上の点C、D、Eなどと作る角(∠ACB、∠ADB、∠AEB)を円周角といいます。
ABを結ぶ線分を「弦」といいますが、1つの弦の同じ側に立つ円周角はどの位置にあっても
大きさは等しく、しかも、円周角は、中心角の半分の大きさです。
さて、正九角形の場合、1つの辺に対する中心角は40°なので、円周角は20°です。
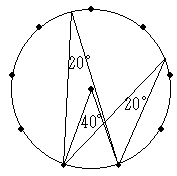
頂点を1つまたいで2点を選ぶと、そこに立つ円周角は40°です。
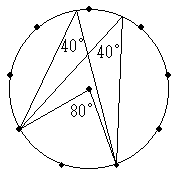
以下、円周角は、60°、80°、100°、120°、140°となります。
以上を踏まえて、問題の答えです。
(1)
100°を持つ三角形は以下の3個です。
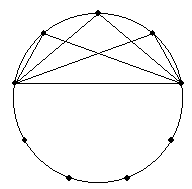
120°を持つ三角形は以下の2個です。
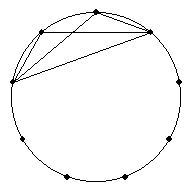
140°を持つ三角形は以下の1個です。
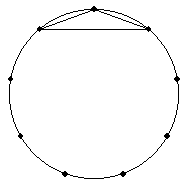
1つの三角形が見つかると、それを40°ずつ回転していけば、
9つの三角形ができます(ただし、正三角形は3つだけ)。
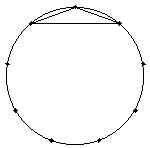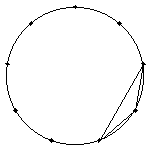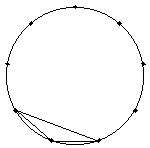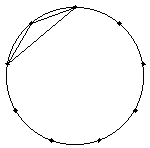
よって、鈍角三角形の個数は、
(3+2+1)×9=54 答え 54個
(2) 内角が20°、40°、120°の三角形は、以下の2個。
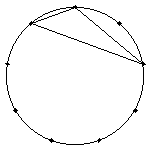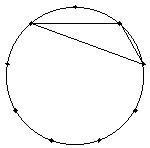
それぞれ9個ずつあるので、
2×9=18 答え 18個
「算数・数学」の部屋に戻る