問題
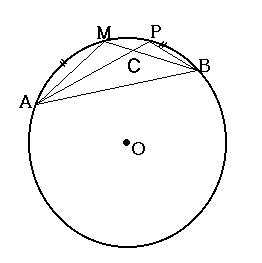
円Oの弧ABの中点をM、弧AB上のM以外の点Pをとる。
このとき、AP+BP<AM+MBを示しなさい。
解答
MBとAPの交点をCとします。
円周角より、∠AMC=∠BPC ∠MAC=∠PBC より、
△AMCと△BPCは相似。
また、半円周≧弧AM=弧BM>弧BPより、
AM>BP
よって、△AMCと△BPCの相似比を
AM:BP=m:1 (m>1)
とおける。
ここで、
BP+PC−BC=k (k>0) (三角不等式より)・・・(1)
とおくと、
AM+MC−AC=m(BP+PC−BC)=mk ・・・(2)
とおける。
(2) から (1) を引いて、
AM+MC+BC−(BP+PC+AC)=(m−1)k
AM+MB−(AP+BP)=(m−1)k>0
となり、
AP+BP<AM+MB
が示された。
算数・数学の部屋に戻る