Hiroya さんからの質問１

問題
△ＡＢＣがあり、４点Ｐ，Ｑ，Ｒ，Ｓをそれぞれ、ＡＣ上、ＡＢ上、ＡＢ上、ＢＣ上にとり、
四角形ＰＱＲＳが
　ＰＱ＝２ＰＳ
を満たす長方形になるように作図せよ。

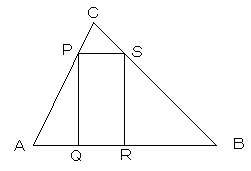
解答１


解答２

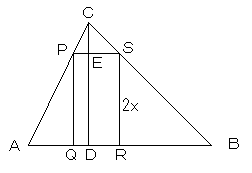
ＣからＡＢに下ろした垂線の足をＤとし、ＰＳ＝ｘ、ＰＱ＝２ｘ とします。
△ＡＢＣと△ＰＳＣの相似より、
　ＡＢ：ＣＤ＝ｘ：(ＣＤ−2x)
よって、
　ＣＤ・ｘ＝ＡＢ(ＣＤ−2x)
　(２ＡＢ＋ＣＤ)ｘ＝ＡＢ・ＣＤ
よって、
　ｘ＝ＡＢ・ＣＤ/(２ＡＢ＋ＣＤ)
ここで、ＣＥ＝ＣＤ−2x　より、
　ＣＥ＝ＣＤ(２ＡＢ＋ＣＤ)/(２ＡＢ＋ＣＤ)−2ＡＢ・ＣＤ/(２ＡＢ＋ＣＤ)
　　　＝ＣＤ²/(２ＡＢ＋ＣＤ)
ＣＤ/2＝ａ とおくと
　ＣＥ＝４ａ²/２(ＡＢ＋ａ)＝ａ・ＣＤ/(ＡＢ＋ａ)
つまり、ＣＤ を ａ/(ＡＢ＋ａ)　倍すれば、ＣＥの長さが出ます。

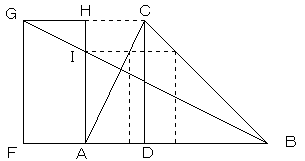
図のように、点Ａを１つの頂点として、長方形ＡＦＧＨを描きます。
ただし、ＧＦ＝ＣＤ、ＧＨ＝ＣＤ/2 とします。
ＢＧとＡＨの交点をＩとすると、ＨＩ が ＣＥに等しくなります。
Ｉ の高さで、長方形ＰＱＲＳを描けば、求める長方形が得られます。


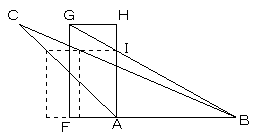
図のような場合も、同様です。

算数・数学の部屋に戻る