Toshiさんからの質問６

問題
△ABCの頂点Aにおける外角の２等分線が、
辺BCの延長および外接円とそれぞれD、Eで交わるとすると
(1) AB・AC=AD・AE
(2) AD²=BD・CD-AB・AC
であることを証明せよ。

解答

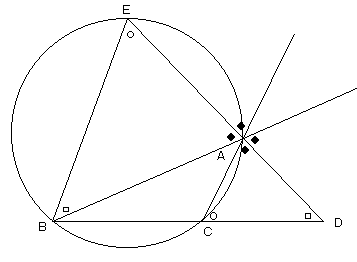
図の●、○、□はそれぞれ等しい角です。
(1)
△ＡＣＤと△ＡＥＢの相似より、
　ＡＣ：ＡＥ＝ＡＤ：ＡＢ
よって、
　ＡＢ・ＡＣ＝ＡＤ・ＡＥ
(2)
方べきの定理より、
　ＢＤ・ＣＤ＝ＡＤ・ＥＤ
また、(1) の結果より、
　ＡＢ・ＡＣ＝ＡＤ・ＡＥ
よって、
　ＢＤ・ＣＤ−ＡＢ・ＡＣ＝ＡＤ・ＥＤ−ＡＤ・ＡＥ
　　＝ＡＤ（ＥＤ−ＡＥ）＝ＡＤ・ＡＤ＝ＡＤ²

算数・数学の部屋に戻る