カズさんからの質問１
問題

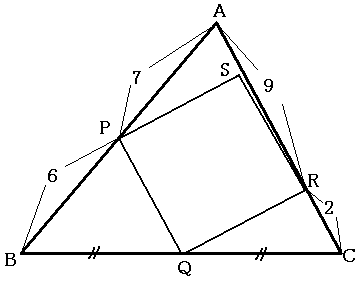
図のように三角形ＡＢＣの内部に正方形ＰＱＲＳが3点Ｐ、Ｑ、Ｒで接していて、ＢＱ＝ＱＣです。
このとき、正方形ＰＱＲＳの面積を求めなさい。

解答

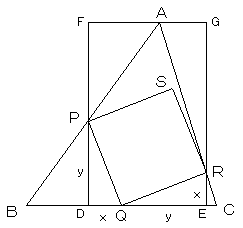
点Ｐ、ＲからＢＣに下ろした垂線の足を、それぞれＤ，Ｅとします。
△ＤＰＱと△ＥＱＲは合同であり、図のように
　ＤＱ＝ＥＲ＝ｘ，　ＤＰ＝ＥＱ＝ｙ
とおきます。さらに、点Ａを通り、ＢＣに平行な直線上に点Ｆ、Ｇを、四角形ＤＦＧＥが
長方形になるように取ります。
　ＤＦ＝(13/6)ｙ　ＥＧ＝(11/2)ｘ
より、
　(13/6)ｙ＝(11/2)ｘ
　ｘ：ｙ＝13：33

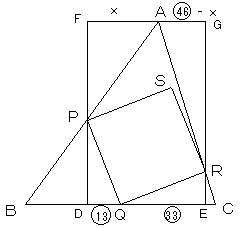
ここで、ＤＱ＝13、ＱＥ＝33 とおき、ＡＦ＝ｘ とおくと、ＡＧ＝46-x とおけます。
　ＢＤ＝(6/7)ＡＦ＝6x/7
　ＥＣ＝(2/9)ＡＧ＝(92-2x)/9
ＢＱ＝ＱＣ　より、
　6x/7＋13＝33＋(92-2x)/9
これを解いて、
　ｘ＝28
よって、ＢＤ＝6x/7＝24

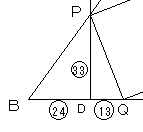
図のように、辺の長さを決めると、
　ＰＱ＝√(13²＋33²)＝√1258
　ＰＢ＝√(24²＋33²)＝√1665
よって、ＰＱはＰＢの
　√(1258/1665)＝√(34/45)　(倍)
ＰＢ＝６より、
　ＰＱ＝2√(34/5)
正方形ＰＱＲＳの面積は
　ＰＱ²＝136/5＝27.2

答え　27.2