問題
半径rの扇形OABがある。
角BOA=90度で、AをOに重なるように折りかえした時の折り目をCDとする。
1 CDの長さを求めよ。
2 BOCの周の長さを求めよ。
3 BOCの面積を求めよ。
解答
CDの位置によって、下の2つが考えられます。
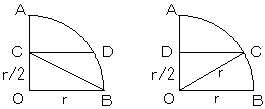
1 上図右において、△DOCは、1:2:√3 の直角三角形である。
よって、CD=(√3)r/2
解答1 点CがAO上にあるとき
2 BO=r、CO=r/2
△OBCにおける三平方の定理より、
BC=(√5)r/2
よって、△BOCの周の長さは (3+√5)r/2
3 △BOCの面積は
BO×CO÷2=r2/4
解答2 点Cが弧AB上にあるとき、
2 ∠BOC=∠OCD=30°であるので、
BO=CO=r、弧BC=2πr/12=πr/6
よって、扇形BOCの周の長さは (2+π/6)r
3 扇形BOCの面積は
πr2/12
算数・数学の部屋に戻る