問題
縦6cm、横8cmの長方形の対角線と長方形の縦、横に接する2つの円を描いた。
円の中心を各O,O’とする。また、対角線に接する点をP,Qとする。
(1) 線分P,Qの長さは何cmか
(2) 線分O,O‘の長さは何cmか
解答
(以下、長さの単位は cm、面積の単位はcm2です)
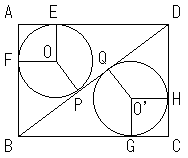
(1)
図のようにA〜Hの記号を付けます。
条件より、AB=CD=6、AD=BC=8
また、三平方の定理より、BD=10 です。
まず、内接円の半径 r を求めます。
△ABDの面積は
△ABD=6×8÷2=24
一方、△ABDを△AOD,△AOB,△BODに分けると、面積はそれぞれ、
△AOD=AD×OE÷2=4r
△AOB=AB×OF÷2=3r
△BOD=BD×OP÷2=5r
合計して、△ABD=△AOD+△AOB+△BOD=12r
以上を比較して、
r=2
よって、
AE=AF=CH=CG=2
となり、
DQ=DH=CD−CH=6−2=4
BP=BF=AB−AF=6−2=4
よって、
PQ=BD−BP−DQ=10−4−4=2
答え:PQは2cm
(2)
O,O’ は、縦2cm、横4cmの長方形の対角線になるので、三平方の定理より
OO’=√(22+42)=2√5
算数・数学の部屋に戻る