問題
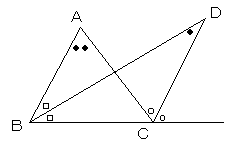
△ABCにおいて、∠Bの二等分線と、∠Cの外角の二等分線の交点をDとするとき、
∠BAC=2∠BDC
であることを証明せよ。
解答
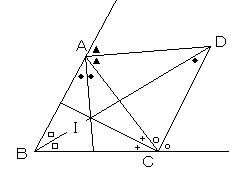
△ABCの3つの内角の二等分線は1点Iで交わり、この点を内心といいます。
△ABCの∠B、∠Cの外角の二等分線を辺BCの外側に引き、その交点は
∠Aの二等分線上にあり、この点を傍心といいます。(点Dは傍心です)
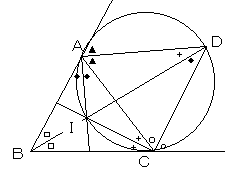
∠IAD=90°、∠ICD=90°より、4点AICDは同一円上にあります。
円周角の定理より、
∠IDC=∠IAC=∠BAC÷2
となり、本題が証明されたことになります。
同様に、∠IDA=∠ACB÷2 の関係も成り立ちます。
算数・数学の部屋に戻る