山本　達也さんからの質問１

問題
n角形の対角線の交点の数は？

解答
３本以上の対角線によって共有される点はないものとします。
また、凹部のない多角形とします。

解法その１
ｎ角形のｎ個の頂点のうち４個を選ぶと、その４点で四角形が１つ出来、その対角線の交点が１つ
存在する。
よって、ｎ個から、４個を選ぶ組み合わせで、
　_nＣ₄＝n(n-1)(n-2)(n-3)/24

解法その２

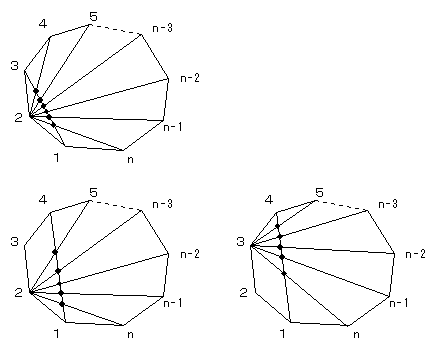
各頂点に１〜ｎまでの番号をふります。
点１から点３に引いた対角線と交わる対角線は、
点１と点３の間にある点２と、点３と点１の間にある、点４、点５・・・点ｎ とを結んだ対角線で、
　１×（ｎ−３）　本　（図の上）
点１から点４に引いた対角線と交わる対角線は、
点２から引いたものが　ｎ−４本、点３から引いたものが同じくｎ−４本で、
　２×（ｎ−４）　本　（図の下左右）　　　（※つづく）

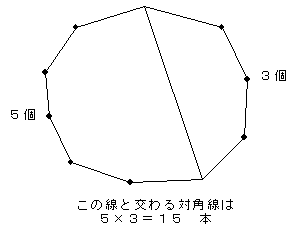
結局、ある対角線を考えるとき、その線によって２つに分けられるそれぞれの頂点の数の積が その対角線と交わる対角線の数になります。

（※つづき）
つまり、点１から引いた対角線によりできる交点は、
　1(n-3)＋2(n-4)＋3(n-5)＋・・・＋(n-5)3＋(n-4)2＋(n-3)1
　　＝Σ_k=1〜n-3k(n-2-k)＝Σ_k=1〜n-3{(n-2)k-k²}
　　＝(n-2)・(n-3)(n-2)/2-(n-3)(n-2)(2n-5)/6
　　＝(n-2)(n-3){(n-2)/2-(2n-5)/6}
　　＝(n-2)(n-3)(n-1)/6
これが、ｎ個の各頂点について言えるので、
　　n(n-1)(n-2)(n-3)/6
ただし、各交点は、４回ずつ数えられている(★)ので、
　　n(n-1)(n-2)(n-3)/24

★例えば、点１と点３を結んだ線と、点２と点４を結んだ線の交点は、
　点１，点２，点３，点４ について考えたときに数えられている。

算数・数学の部屋に戻る