問題
五角形ABCDEにおいて
角A=90度
角B+角D=270度
角C+角E=180度
AB=BC=CD=DE=EA=2cm
この時、五角形ABCDEの面積を求めよ。
解答
まず、この図形をどのように作図するかを考えます。
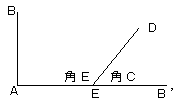
角C+角E=180°なので、図のように点Eに対して点Aと対称な点B’をとると、
∠DEB’が角Cになります。
BD=B’Dになれば、五角形ABCDEが出来ます。
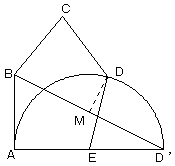
BD’の垂直二等分線上でEから距離2の点をDに取り、BC=DC=2となる点Cを取ります。
五角形ABCDEの面積を求めるかわりに四角形ABDD’の面積を求めます。
さらに△ABD’と△BDD’に分けます。
△ABD’=4×2÷2=4
点Eを原点に取り、MDの式を
y=2x+1
図の半円の式を
x2+y2=4
として解くと、Dの座標は((√19−2)/5, (2√19+1)/5)
MをBD’の中点とすると、M:(0,1)
MD=√{(23−4√19)/5}=(√19−2)/√5
BD’=2√5
よって
△BDD’=√19−2
よって、
五角形ABCDE=四角形ABDD’=4+√19−2=2+√19
算数・数学の部屋に戻る