問題
一辺の長さ2の正三角形ABCの辺AB,BC,CA上にそれぞれ点 P,Q,R を
AP=BQ=CR≦1
となるようにとる。△PQRの面積が△ABCの面積の1/2倍となるときのAPの長さをもとめよ。
解答
AP=2x とおきます。
※2x とおくのは、途中で分数が出ないようにするためのテクニックです。AP=x とおいてもできます。
まず、面積が1/2倍になるためには、辺の長さは√2/2倍でなければ
ならないので、PQ=QR=RP=√2 となることを押さえた上で、
解答1(三角関数を用いた方法)
△APRにおいて、第2余弦定理
PR2 = AP2 + AR2 -2AP・ARcos∠PAR
より、
(√2)2 = (2x)2 + (2-2x)2 -2(2x)(2-2x)cos60°
cos60°= 1/2 を用いて、式を整理すると、
12x2- 12x + 2 = 0
6x2- 6x + 1 = 0
2次方程式の解の公式より、
x = (3 ±√3)/6
AP<1 より、x<1/2 だから
x = (3 - √3)/6
AP = 2x = (3 - √3)/3
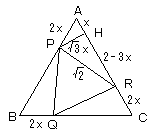
解答2(三平方の定理を用いた方法)
図のように、点PからACに垂線をおろし、その足を点Hとします。
∠PAR=60°なので、
AH=x
PH=√3x
また、
HR=AC - CR - AH = 2 - 3x
△PHR において、三平方の定理より、
PH2 + HR2 = RP2
(√3x)2 + (2-3x)2 = (√2)2
整理して
12x2- 12x + 2 = 0
6x2- 6x + 1 = 0
2次方程式の解の公式より、
x = (3 ±√3)/6
AP<1 より、x<1/2 だから
x = (3 - √3)/6
AP = 2x = (3 - √3)/3
「算数・数学」の部屋に戻る