∠ABR=∠RBPであるときに、BPの長さを求めなさい。
解答
里奈さんからの質問
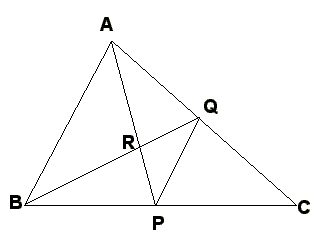
問題
次の図でAB=5cm、BC=8cm、CA=7cm、ABとQPが平行、
∠ABR=∠RBPであるときに、BPの長さを求めなさい。

解答
条件より、BQは、∠ABCの2等分線です。
まず、「角の2等分線の定理」というものを証明します。
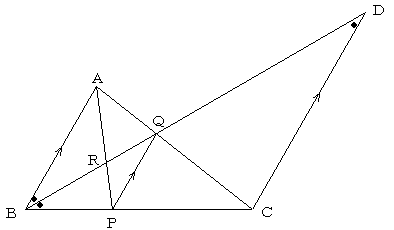
図のように、点Cを通り、ABに平行な直線と、BQの交点をDとすると、
AB//CDより、
∠ABR=∠QDC
また、条件より、
∠ABR=∠RBP
よって、
∠RBP=∠QDC
以上より、BC=CD
一方、△ABQと△CDQの相似性より、
AB:CD=AQ:CQ
以上より、
AQ:CQ=AB:BC
つまり、「角の2等分線の定理」とは、
△ABCにおいて、∠ABCの2等分線と、ACの交点をQとするとき、
AQ:CQ=AB:BC
さて、問題に戻ると、
角の2等分線の定理より、
AQ:QC=AB:BC=5:8
一方、AB//QP より、
AQ:QC=BP:PC=5:8
よって、BP=BC×(5/13)=40/13・・・答え
別解
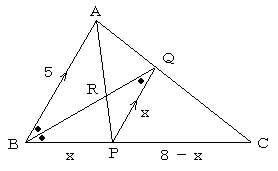
図のように、∠ABR=∠RBP=∠RQP より、
BP=PQ
一方、△ABCと△QPCの相似性より、
AB:QP=BC:PC
BP=PQ=χ とおくと、
5 : χ = 8 : (8−χ)
よって、
8χ=5(8−χ)
8χ=40−5χ
13χ=40
χ=40/13・・・答え