みゅゥさんからの質問３

２問あります。

問題１
∠ＢＡＣ＝９０°の直角三角形ＡＢＣがあり、ＡからＢＣにおろした垂線の足をＨとする。
　i) △ＡＨＣの外接円を描くことにより、ＢＡ²＝ＢＨ・ＢＣを方べきの定理を用い証明せよ。
　ii) 適当な円を描くことにより、ＡＨ²＝ＢＨ・ＨＣを方べきの定理を用い証明せよ。

証明
　i)
　
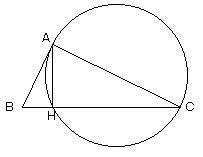
　方べきの定理より、ＢＡ²＝ＢＨ・ＢＣ
　※これはむしろ、方べきの定理そのものであり、それを証明するために△ＡＢＨと△ＣＢＡ
　　の相似より、ＢＡ：ＢＨ＝ＢＣ：ＢＡ。これより、ＢＡ²＝ＢＨ・ＢＣ とすべきものです。

　ii)
　
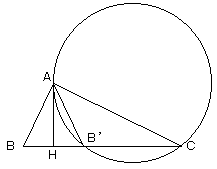
　ＨＣ上に、点Ｂ' を ＨＢ＝ＨＢ' となるように、とります。△ＡＢ'Ｃの外接円を描きます。
　∠ＡＣＢ'＝∠ＨＡＢ' より、接弦定理より、ＨＡはこの円の接線となります。
　方べきの定理より、ＡＨ²＝ＢＨ・ＨＣ

問題１の結果をユークリッドの定理ということにします。

問題２
　i) ユークリッドの定理を用いて三平方の定理ＢＣ²＝ＡＢ²＋ＣＡ²を証明せよ。
　ii) ユークリッドの定理ＡＢ・ＡＣ＝ＢＣ・ＡＨ（＝２・三角形ＡＢＣ）を利用して、 １/ＡＢ²＋１/ＣＡ²＝１/ＡＨ²を証明せよ。

証明
　i) ＢＡ²＝ＢＨ・ＢＣ、ＡＨ²＝ＢＨ・ＨＣ を辺々引いて、
　　ＢＡ²−ＡＨ²＝ＢＨ（ＢＣ−ＨＣ）＝ＢＨ²
　　よって、
　　ＢＡ²＝ＡＨ²＋ＢＨ²
　　これで、△ＡＢＨについての三平方の定理が示されました。
　　あくまでも、△ＡＢＣにおいて示すなら、相似比 BC/AB=AC/AH=AB/BH の２乗を掛けて、
　　ＢＣ²＝ＡＢ²＋ＣＡ²
　　を示すことができます。
　ii) i) で示した ＢＣ²＝ＡＢ²＋ＣＡ² の両辺を (ＡＢ・ＡＣ)²＝(ＢＣ・ＡＨ)² で割って、
　　ＢＣ²/(ＢＣ・ＡＨ)²＝ＡＢ²/(ＡＢ・ＡＣ)²＋ＣＡ²/(ＡＢ・ＡＣ)²
　　よって、 １/ＡＢ²＋１/ＣＡ²＝１/ＡＨ²

「算数・数学」の部屋に戻る