問題
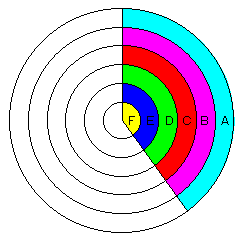
図のように中心を共有する6つの円がある。各円の半径の差は全て
等しく、また円Fの半径とも等しいとする。A、B、C・・・はそれぞれの部分
の面積を表している。
このとき、次の式の答えをAからFを使って表しなさい。
1)D+E+F=
2)A+D-B=
3)C×E-A-B=
4)(A+B)÷(E+F)=
5)(2A+B)÷(E+F)=
6)((D+F)× C+B )÷E
解答
Fの面積を1とすると、
FとEを合わせた扇形は、Fと相似で、相似比は2倍なので、面積は4倍。
よって、EはFの(4−1=)3倍。
同様に、F+E+Dの面積は(3×3=)9倍。
よって、Dの面積は、(9−4)=5倍。
同様に調べると、
A:B:C:D:E:F=11:9:7:5:3:1
となる。
そこで、A=11F,B=9F,C=7F,D=5F,E=3F とおく。
1) D+E+F=5F+3F+F=9F=B
2) A+D−B=11F+5F−9F=7F=C
3) 面積どうしを掛けることは出来ません
※正確には、面積どうしを掛けたものと面積とのたし算ひき算が出来ません。
4) (A+B)÷(E+F)=20F÷4F=5
5) (2A+B)÷(E+F)=31F÷4F=31/4
6) 括弧を追加します。
((D+F)×(C+B))÷E=6F×16F÷3F=32F=A+B+C+D(?)
算数・数学の部屋に戻る