理科の実験で使用するビーカーを想像してください。
開口部にも底の部分にもR部分があります。
それぞれのR(半径)をr1、r2 とし、高さh、直径dの場合の体積を出す方程式をお教えください。
C:x=t-sint, y=1-cost (0≦t≦2π)がある。
傾き-1/√3の直線Lが曲線Cと点Pで接している。
(1)接線Pの座標と直線Lの方程式を求めよ。
(2)曲線と直線およびX軸の x≧2π の部分とで囲まれた図形の面積Sを求めよ。
の表面積を求めよ。
2つの円柱の重なった部分の立体について、
(1)体積を求めよ。(横に輪切りにしてカバリニリの原理を使う、半径1の球の体積との比)
(2)葉っぱのような図形を4枚つなげれば、この立体をつくることが出来る。この葉っぱの形を調べよ。(曲線を関数の式として表せ)
放物線 C:y=x2に点Pから2本の接線、L、Mを引く時、C,L,Mで囲まれる図形の面積が常に18となるような点Pの軌跡を求めよ。
問2.
曲線y=x4−2x2+x上のある点における接線Gが曲線上の他の点で再び接している。
(1) 2つの接点の座標、及び接線Gの方程式を求めよ。
(2) 曲線と接線Gとで囲まれた図形の面積を求めよ。
問3.
2つの曲線y=x(x−1)2、y=kx2 (k>0)について、次の問に答えよ。
(1) この2つの曲線は相異なる3点で交わることを示せ。
(2) この2曲線で囲まれる2つの図形の面積が等しくなるような k の値を求めよ。
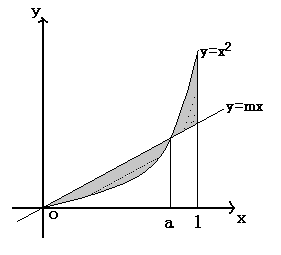 |
m(0<m<1)を変化させて、灰色の部分の面積が最小になるようにします。 このとき、a の値を求めなさい。 |
(1)f(x)がx≧0で単調増加するような点(a,b)の範囲Gを図示せよ。
(2)x≧0におけるy=f(x)の逆関数をx=f-1(y) (x≧0)とする。点(a,b)がGを動くとき
定積分
(底面積)×(高さ)÷3
を証明せよ。
mが奇数、n が n≠0の偶数であるとき、次の値はいくらですか?
問題2
とする時、
(1)A+B を求めよ。
(2)AおよびBを求めよ。
また、円C上に頂点Aを持つ放物線y=-(x-p)2+qをC2とする。
(1)C2の頂点Aが原点以外にある時、C1とC2は異なる2点で交わることを示し、その交点のx座標を求めよ。
(2)C1とC2によって囲まれる図形の面積をSとする。C2の頂点Aが円C上を動くとき、Sの最大値とそのときのAの座標を求めよ。
dc/dt=αS−βc
のような関係がある。α、β、S はいずれも定数であるとき、関数 c=f(t) を求めよ。
ただし、f(0)=0 とする。
曲線 y=x+2sinx と x軸 、および直線 x=2π で囲まれた部分の面積を求めよ。
また、その部分を x軸のまわりに回転してできる回転体の体積を求めよ。
問題2
自然数nに対し、In=∫(1〜e)(logx)^n dxとおく。
部分積分法を使ってIn=e−nIn-1を示せ。またI1 I2 I3 I4を求めよ。
と、x軸とで囲まれる部分をD1とし、4点O(0,0),A(4,0),B(4,4),C(0,4)を頂点とする正方形の内部と周をD2とする。
(1)放物線Cはaの値によらず直線 y=[ア]x/[イ] + [ウ]に接する。
(2)D1⊆D2となるようなaの範囲は、0<a≦√[エオ] − [カ] である。
(3)D1∩D2の面積S(a)はa=[キ]/[ク]のとき、最大値[ケコ]/[サ]をとる。
半径r、中心角∠AOB=2θ、弧AB=2a、弦AB=2b とすると
扇形の重心Gは扇形の対称軸上にあり、中心Oから 2rb/3a の
距離にある点であることを示せ。
またこの直線と2つの放物線とで囲まれた部分の面積を求めよ。
接線との交点のy座標は1である。
(1)a,b,c,を求めよ。
(2)この放物線と(0,0)における接線(2,-2)における接線により囲まれる図形の面積を求めよ。
(1) 放物線上の点(a,a2-2a+4)における接線の方程式をy=px+qの形で表せ。
(2) (1)で求めた接線が原点を通るとき、その接線の方程式を求めよ。
(3) (2)の2本の接線と放物線で囲まれた図形の面積を求めよ。